对抗样本（九）C&W’s Attack

一、论文相关信息

  1.论文题目

     Towards Evaluating the Robustness of Neural Networks

  2.论文时间

    2016年

  3.论文文献

     https://arxiv.org/abs/1608.04644

二、论文背景及简介

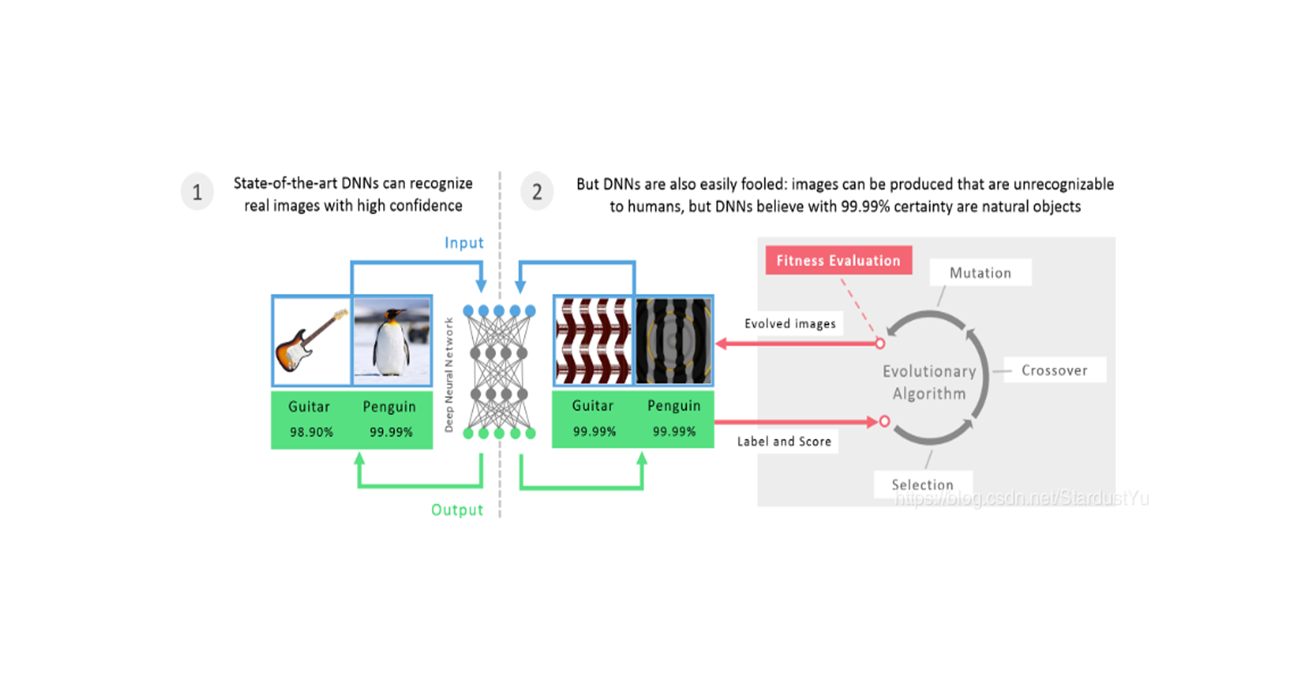
   对抗样本的出现使得神经网络难以应用到安全相关的领域，防御性网络蒸馏能够训练一个专有网络，提高网络的鲁棒性，降低其被攻击的成功率从95%到0.5%。

   这篇论文证明蒸馏网络并不能够显著的提升网络的鲁棒性，同时引入了三种攻击方法，能够以100%的成功率攻击蒸馏网络和未蒸馏网络。这三种方法是根据三种距离($ l_0,l_2,l_{\infty}$ )得到的。相比于之前的攻击方法，该攻击方法更有效率。

三、论文内容总结

• 将原对抗目标进行修改，并平滑了box constrained，使其可以直接通过梯度下降方法来对目标进行优化。
• 系统的评估了在生成对抗样本路上的目标函数的选择，这种选择能够极大的影响攻击的效率
• 提出对抗目标中的常数$ c$ 是非常重要的，并提出了一种该常数$ c$ 的方法
• 提出直接对离散化的图像（范围在[0,255]，而不是[0,1]）进行攻击能够得到更好的效果
• 基于$ L_0,L_2,L_{\infty}$ 距离，得到了三种攻击方法，这些攻击方法更有效率。其中$ L_0$ 攻击方法是目前为止第一个可以攻击ImageNet的目标攻击方法
• 采用了迭代式的方式，巧妙地解决了$ L_0、L_{\infty}$ 在作为目标函数时的不可导的问题
• 这三种攻击方法可以100%的攻击蒸馏后的网络
• 使用高置信度的对抗样本作为迁移测试集来评估防御方法
• 在迁移前，采用更强的分类器作为攻击对象，其生成的对抗样本的迁移性越好。

附：如需继续学习对抗样本其他内容，请查阅对抗样本学习目录

四、论文主要内容

1. Introduction

   一般来说，有两种用来评估神经网络鲁棒性的方法：第一种是试图证明一个下界，第二种是找到一个上界。第一种方法在实际操作实现时比较困难，都需要进行一些估计。但是使用上界的话，对于一些攻击能力差的攻击方法来说，上界则没什么用处了。

   在这篇论文中，作者进行了大量的攻击，可以被用来找到上界，同时，基于$ L_0,L_2,L_{\infty}$ 距离，得到了三种攻击方法，这三种攻击方法，可以100%的攻击蒸馏后的网络。这也证明蒸馏网络虽然可以抵御之前的攻击方法得到的对抗样本，但对于一些更强大的攻击方法来说，依旧无能为力。

   作者也证明到，从一个未防御的网络用该方法生成的对抗样本可以迁移到蒸馏后的网络中。

2. Background

   简要的介绍了一下对抗样本领域的一些知识点。

   对对抗样本中目标类的选择方法而言，有以下三种情况：

• 平均情况：随机的选择一个目标类
• 最好地情况：对每一个类别进行攻击，找到最容易攻击的类别

• 最坏的情况：对每一个类别进行攻击，找到最难攻击的类别

     距离计算方法：

• $ L_0$ 距离表示的是对抗样本相对于原始样本改变的像素的数目

• $ L_2$ 距离表示的是对抗样本与原始样本的欧氏距离，旨在使得对抗扰动最小
• $ L_{\infty}$ 距离计算的是单个像素扰动的最大值

$$||x-x'||_{\infty} = max(|x_1-x_1'|,...,|x_n,x_n'|)$$

   这三种距离公式都不是人类感知相似度的度量，我们无法判断哪一个距离公式对于生成对抗样本而言是最优的。创造一个好的距离公式是非常重要的。

3. Attack Algorithms

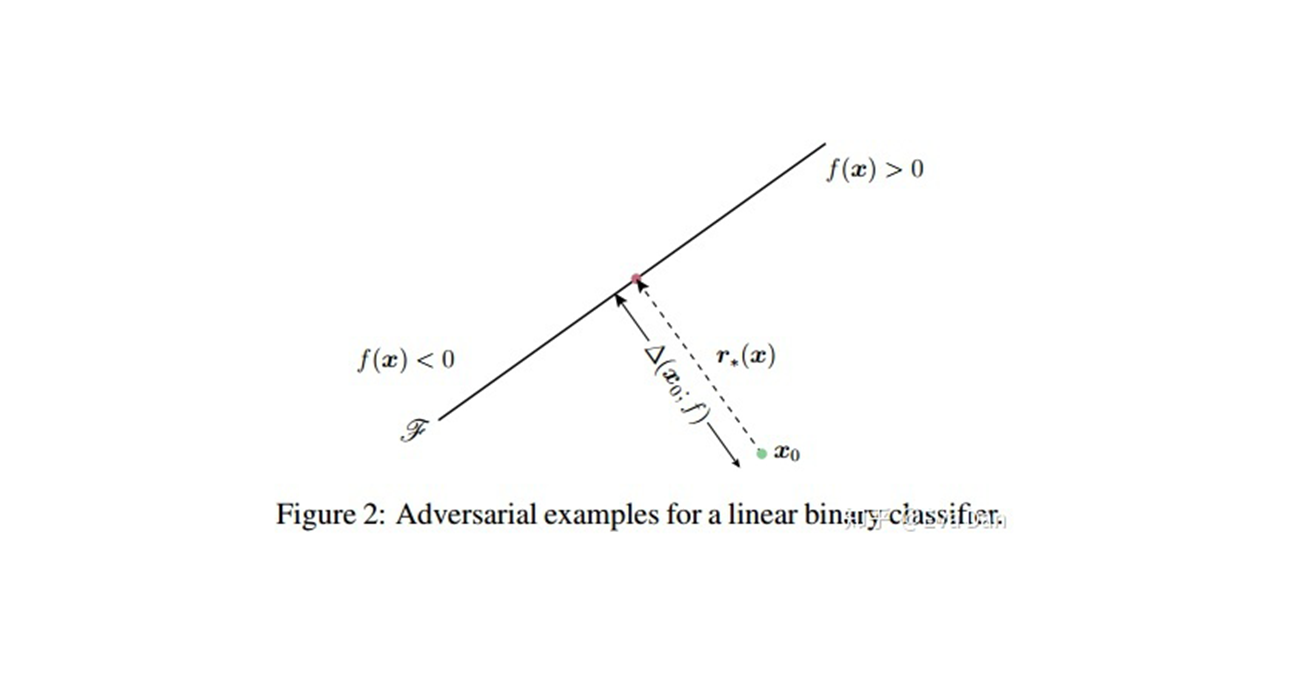
   简要的回顾了之前的攻击方法L-BFGS，FGSM，JSMA，Deepfool

   其中L-BFGS和Deepfool是基于$ L_2$ 距离进行优化的。FGSM是基于$ L_{\infty}$ 进行优化的，JSMA是基于$ L_0$ 进行优化的。

4. Experimental Setup

   作者所采用的网络模型、数据集如下：

   在ImageNet数据集下采用预训练模型Inceptionv3.

   在MNIST下准确率99.5%，在CIFAR-10下准确率80%，在ImageNet下96%的top-5准确率

5. Our Approach

   首先，先给出对抗样本的最基本的优化方程

$$\begin{equation} \begin{split} min &\qquad D(x,x+\delta)\\ s.t. &\qquad C(x+\delta)=t \\ &\qquad x+\delta \in [0,1]^n \\ \end{split} \end{equation}$$

   其中$ D$ 表示距离标准，$ \delta$ 表示对抗扰动，$ C$ 表示神经网络，$ t$ 表示目标类别。

   我们可以把他看成一个优化问题，采用目前的优化算法来进行解决。

A. Objective Function

   上面的公式对于目前的优化算法来说，直接处理太困难了，因为$ C(x+\delta)=t$ 这个条件是非线性的。所以我们把他表达成了不同的形式，一个更容易优化的形式。

   我们定义一个目标函数$ f$ ，当且仅当$ f(x+\delta)\le0$ 时，$ C(x+\delta)=t$ 。下面是一些可能采取的选择：

$$\begin{equation} \begin{split} f_1(x')= & -loss_{F,t}(x')+1\\ f_2(x')= & (max_{i\ne t}(F(x')_i) - F(x')_t)^+\\ f_3(x')= & softplus(max_{i\ne t}(F(x')_i) - F(x')_t) - log(2)\\ f_4(x')= & (0.5-F(x')_t)^+\\ f_5(x')= & -log(2F(x')_t-2)\\ f_6(x')= & (max_{i\ne t}(Z(x')_i) - Z(x')_t)^+\\ f_7(x')= & softplus(max_{i\ne t}(Z(x')_i) - Z(x')_t) - log(2)\\ \end{split} \end{equation}$$

   其中$ s$ 代表原始类别，公式$ (e)^+$ 表示$ max(e,0)$ ，公式$ softplus(x)=log(1+exp(x))$ ，$ loss_{F,s}(x)$ 表示交叉熵损失函数。$ F(x’)_i$ 表示经过神经网络以及softmax的第$ i$ 个输出值，$ Z(x’)_i$ 表示经过神经网络后的logits的第$ i$ 个输出值。

   有了上面的目标函数后，我们就可以改变优化目标为：

$$\begin{equation} \begin{split} min &\qquad D(x,x+\delta)\\ s.t. &\qquad f(x+\delta) \le 0 \\ &\qquad x+\delta \in [0,1]^n \\ \end{split} \end{equation}$$

   进一步的，我们可以修改为：

$$\begin{equation} \begin{split} min &\qquad D(x,x+\delta)+c·f(x+\delta)\\ s.t. &\qquad x+\delta \in [0,1]^n \\ \end{split} \end{equation}$$

   其中$ c>0$ 是适当选择的常数。这两个是等价的，因为存在$ c>0$ ，使得后者的最优解与前者的最优解相匹配。

   如果我们的距离标准$ D$ 采用$ l_p$ norm，那么我们的问题就变为：

$$\begin{equation} \begin{split} min &\qquad ||\delta||_p+c·f(x+\delta)\\ s.t. &\qquad x+\delta \in [0,1]^n \\ \end{split} \end{equation}$$

   我们如何选择c呢？通常来说最有情况是选择一个能够使$ f(x*)\le 0$ 的最小的c。但是这样做，梯度下降需要优化$ \delta$ 和$ c$ ，来找到最好地$ c$ ，这会非常耗时。

   作者在MNIST数据集上做了实验，采用$ c=[0.01,100]$ ，其得到的结果如下：

   在实际情况下，作者采用修正的二分搜索的方法寻找$ c$ 。

B. Box constraints

   为了确保我们得到的对抗样本在图片的允许范围内，我们需要满足$ 0\le x_i + \delta_i \le 1$ 。这个限制条件在优化问题上被称之为”box constraints”。之前是通过L_BFGS方法来解决这个问题的，作者列举了三种解决这个问题的方法：

1. Projected gradient descent。该方法是在进行一次梯度下降后，将$ x_i$ clip到box区域内。这个方法不太好，其更新操作太复杂，因为每次更新$ x_i$ 后，下一次迭代的输入就变了
2. Clipped gradient descent。该方法并不是clip$ x_i$ ，他是把clip操作融合到了目标函数上，也就是说，他将原函数$ f(x+\delta)$ 修改为了$ f(min(max(x+\delta,0),1))$ 。虽然这解决了上面的问题，但是却引来了一个新的问题，这个算法可能会get stuck，陷入一个平坦点，在该点上梯度不为0的地方可能超出了box，这样即使再怎么增加分量$ x_i$ 也不会跳出该点。
3. Change of variables。该方法引入了一个新的变量$ w_i$ ，网络对$ w_i$ 进行优化：

$$\delta_i = \frac{1}{2}(tanh(w_i)+1)-x_i$$

   经过这样的转换后，可以和你清楚的看到，$ -1\le tanh(w_i)\le 1$ ，且$ w_i$ 不限范围。我们可以把它看作一种clipped gradient descent的平滑方法，其消除了get stuck的问题。

   使用第三种方法，我们就饿绝了box constraints的问题，这样我们就可以采用一些常用的梯度下降算法来进行求解了。

C. Evaluation of approaches

   该方法的第一步就是选择常数$ c$ ，作者总共执行了20轮二分搜索，对每一个选中的$ c$ ，作者都会用Adam执行10000次梯度下降。然后找到一个最好地$ c$ 。

   我们采用不同的损失函数$ f$ ，其得到的结果如下：

   为什么有些损失函数好，而有些不好呢？作者认为，当$ c=0$ 时，我们只优化$ D$ loss，那么得到的结果肯定是扰动为0，当$ c$ 很大时，梯度下架就会以贪婪的方式沿着减小$ f$ loss的方向走，这样就忽略了$ D$ loss，这就造成梯度下降只能找到局部最优解。

   也就是说，常数$ c$ 有着跟$ D$ loss项和$ f$ loss项同样的地位，同样重要。

   我们根据结果可以看到$ f_1$ 和$ f_4$ 的效果并不好，那么是为什么呢？因为其特性，导致常数$ c$ 并不与他匹配，下面我们来证明一下。

   我们在每一次梯度下降后都会有一点对样本更新$ \epsilon$ ，该变动需要让我们的目标函数变小，也就是该$ \epsilon$ 需要满足：

$$\epsilon < c(f_1(x+\epsilon)-f(x))$$

   当变化足够小时，即$ \epsilon \to 0$ 时，上式可以变化为：

$$\frac{1}{c} < |\nabla f_1(x)|$$

   也就是说，$ c$ 必须要满足比梯度的倒数要大。但是对于$ f_1$ 和$ f_4$ 而言，采用交叉熵损失函数后，其梯度非常小，也就是说最优$ c$ 需要非常大的值，当$ \epsilon$ 稍微有点变动时，最优$ c$ 需要变化很多，这就导致，我们所采用的常数$ c$ 非常不适合这两个目标函数，所以其结果就不是很好。

D. Discretization(离散化)

   这一部分主要是说明，我们通过将[0,255]区间的像素值转化到了[0,1]区间内进行求解，这稍微的降低了我们得到的对抗样本的质量。

   如果不想要降低这部分质量，仍然采用[0,255]的图像，我们可以在图像上进行贪婪搜索，每次只改变一个像素值。

   本文的方法因为能够找到更小的扰动，所以离散化带来的影响时不能忽略的。

6. Our Three Attacks

   把这些想法放到一起，就得到我们最后的方法。

A. Our $ L_2$ Attack

   给定样本$ x$ ，我们选择一个目标类$ t$ ，那么我们要做的就是找到变量$ w$ ，满足：

$$min\quad ||\frac{1}{2}(tanh(w)+1)-x||_2^2+c·f(\frac{1}{2}(tanh(w)+1))$$

   其中$ f$ 采用$ f_6$ ，即$ f(x’)=max(max{Z(x’)_i:i\ne t}-Z(x’)_t,-\kappa)$ 。我们可以通过调整$ \kappa$ 来控制对抗样本的置信度，$ \kappa$ 可以使对抗样本拥有更高的置信度。不过，在我们的实验中，采用$ \kappa=0$ 。

   还有一个问题就是，之前我们说过，我们采用离散化的方式，所以在梯度下降中采用贪婪搜索时会有一些问题，它没有被证明一定能找到最优解，可能会陷入局部最优。因此我们在原始图像中随机选择多个开始点进行梯度下降。我们从半径为r的球均匀地随机抽取点，其中r是迄今为止发现的最近的对抗性例子。从多个起点出发可以降低梯度下降陷入坏的局部极小值的可能性。

B. Our $ L_0$ Attack

   $ L_0$ 距离是不可导的，因此它并不适合标准的梯度下降方法，我们在这里使用迭代式的算法。

   在每次迭代过程中，都会识别一些对分类器输出没有太大影响的像素点，然后固定这些像素点，即：这些像素点之后不会再改变了。每次迭代后，固定的像素点集会越来越大，在每一次更新了像素点集后，我们都会经过一个消除操作，识别一些 可以通过修改比较小的值 就能够得到对抗样本的 像素点。在每次迭代过程中，我们都会使用我们的$ L_2$ 攻击方法来识别哪些像素是不重要的。

   在每次迭代过程中，我们都会调用$ L_2$ 攻击方法，仅仅修改那些再允许集（固定集的补集）中的像素点，然后我们得到了扰动$ \delta$ ，我们计算梯度，得到$ g = \nabla f(x+\delta)$ ，我们选择像素点$ i = arg min_i g_i·\delta_i$ ，将该像素点固定，并将其从允许集中移出。其中$ g_i·\delta_i$ 表示的是从图像的第$ i$ 个像素点得到的$ f$ 的减少量，减少量越小，表示该像素点对$ f$ 越没有影响。 该步骤不断重复，知道$ L_2$ 攻击再也得不到对抗样本。

   还有一个细节，是用于找到常数$ c$ 的，我们先初始化$ c$ 是一个很小的值，例如$ 10^{-4}$ ，如果$ L_2$ 找不到对抗样本，那么就将$ c$ 乘以两倍，直到$ L_2$ 找到一个对抗样本或者$ c$ 超出了限制（例如$ 10^{10}$）。

   值得注意的是，上面的迭代方法比JSMA更有效率。

C. Our $ L_{\infty}$ Attack

   $ L_{\infty}$ 并不完全可导的，标准的梯度下降方法在该方法上运行的结果很差。因为$ L_{\infty}$ 距离只关心最大的变化点，因此非常容易被困住。例如：我们可能在某次迭代得到的某两个点的扰动为$ \delta_i=0.5,\delta_j=0.5-\epsilon$ ，这时$ L_{\infty}$ 只更新了$ \delta_i$ ，可能在下一次迭代，这两个点变成了$ \delta_i = 0.5-\epsilon’,\delta_j=0.5+\epsilon’’$ ，这个时候$ L_{\infty}$ 只更新了$ \delta_j$ ，因此梯度将会出现震荡的现象，而这种情况将不会取得成功。

   因此，我们也采用迭代式的算法求解。我们为每一个扰动添加一个惩罚项$ \tau$ （初始化为1，随迭代次数慢慢减小），这个惩罚项阻止了振荡现象的产生，因为，此时loss项不再只处理最大的值，而是处理那些大的值，最终目标函数变为：

$$min \quad c·f(x+\delta) + \sum_i[(\delta_i - \tau)^+]$$

   在一次梯度下降得到$ \delta$ 后，通过迭代找到合适的$ \tau$ ，如果所有的$ \delta_i$ 都小于$ \tau$ ，那么就将$ \tau$ 乘以0.9。否则就停止迭代。这种策略解决了上面的$ 0.5,0.5+\epsilon$ 这样微小差别的问题，会把这两个点都加入到loss中去。

   同样的，我们也需要找到一个合适的$ c$ ，这采用了与$ L_0$ 相同的寻找$ c$ 的方案

7. Attack Evaluation

   这一节主要是将论文的方法与之前的经典方法（FGSM、BIM、Deepfool、JSMA）进行对比。

   对一个样本而言，sucess 表示 该方法生成了对抗样本（无论扰动多大，扰动应该会有一个上界值），failure 表示 无论扰动多大都无法生成对抗样本。

   作者使用了CIFAR和MNIST测试机中的1000张图片，使用了ImageNet测试集中的1000张图片（来自于100个类，且被Inceptionv3分类正确的）。

   JSMA因为计算太大，每次迭代只选择图片中的两个点，而ImageNet的图片像素高达299x299x3，计算量太大，我们当作JSMA无法在ImageNet上运行。

8. Evaluating Defensive Distillation

   Defensive distillation是借用蒸馏的方法来提高网络的鲁棒性，进而实现防御，其在网络蒸馏的基础上做了两个改变，第一，蒸馏网络与原网络大小一致，即蒸馏不再是为了减小网络；第二，蒸馏网络的softmax的温度T很高，这保证了蒸馏网络对其预测值更有自信。温度越高，其得到的结果越soft。温度越低，其结果越hard。当温度趋近于0，其结果趋近于hard target。

$$softmax(x,T)_i = \frac{e^{x_i/T} }{\sum_j e^{x_j/T} }$$

   Defensive distillation共有四个步骤：

1. 训练一个网络，在训练阶段，其温度设置为T（高的温度）
2. 遍历数据集，计算每一个样本所对应的soft label，此时温度依旧为T
3. 训练蒸馏网络，尺寸与第一个网络（称为teacher network）相同，使用soft label作为label来训练，温度依旧设置为T
4. 训练完蒸馏网络后，我们就可以用它进行test了，test时采用温度为1

A. 现有攻击方法的脆弱性

   这里，记$ Z(·)$ 表示logits，$ F(·)$ 表示softmax输出。

   我们来分析一下Denfensive Distillation的可行性，由于我们在蒸馏网络用$ T$ 进行训练，而在test时，设置温度为1，这就导致了在test时，softmax的$ x_i/T$ 项增大了$ T$ 倍，所以softmax在原始标签的输出将会非常大，趋近于1，而在其他标签的输出就会非常小。这就导致，softmax在其他标签上的输出的梯度接近于0。

   L-BFGS和Deepfool正是因为这种梯度接近于0而导致其无法攻击对抗样本，因为L-BFGS和Deepfool使用的是最基础的目标函数，而在梯度为0下，该目标函数不可行了。而如果我们把L-BFGS的目标函数替换成我们方法的目标函数，L-BFGS就不会失败，此时，我们可以设置$ F’(x) = softmax(Z(x)/T)$ 来相应的改一下我们方法的目标函数$ loss_{F’,l}(·)$ ，这样梯度就不会消失，就能够正常的进行参数更新。

   JSMA-F（即使用F的输出得到的JSMA）、FGSM，也是因为上面的原因而失败的。

   JSMA-Z（即使用Z的输出得到的JSMA）失败的原因就有一些复杂，可能是因为使用温度T进行训练时，其得到的logits也受到了影响

B. 应用我们的攻击方法

   使用T=100复现了Denfensive Distillation，得到实验结果如下

C. 温度的影响

   在Denfensive Distillation中说明，在MINST上，T=1时，成功率91%；T=5时，成功率24%；T=100时，成功率0.5%。

   当用在我们的实验上的时候，结果如下：

   这也说明，增加温度并不会增加网络的鲁棒性。

D. 迁移性

   我们在一个基础模型上进行攻击，然后将一些置信度高的样本迁移到蒸馏网络中去，观察其成功率。在攻击时，我们采用了目标函数$ f_6$ ，使用了$ L_2$ 攻击：

$$f(x') = max(max\{Z(x')_i:i\ne t\},-k)$$

   其中$ k$ 控制了生成的对抗样本的置信度，$ k$ 越大，置信度越高，其得到的迁移曲线如下：

   之后作者使用一个更弱的分类器作为基础模型进行攻击，其迁移曲线如下：

   也就是说，在迁移前，采用更强的分类器作为攻击对象，其生成的对抗样本的迁移性越好。

9. Conclusion

   这篇论文提出了一个更强的攻击方法，打败了蒸馏网络。