对抗样本（十三）Feature Adversary

一、论文相关信息

  1.论文题目

     Adversarial manipulation of deep representations

  2.论文时间

    2016年

  3.论文文献

     https://arxiv.org/pdf/1511.05122.pdf

二、论文背景及简介

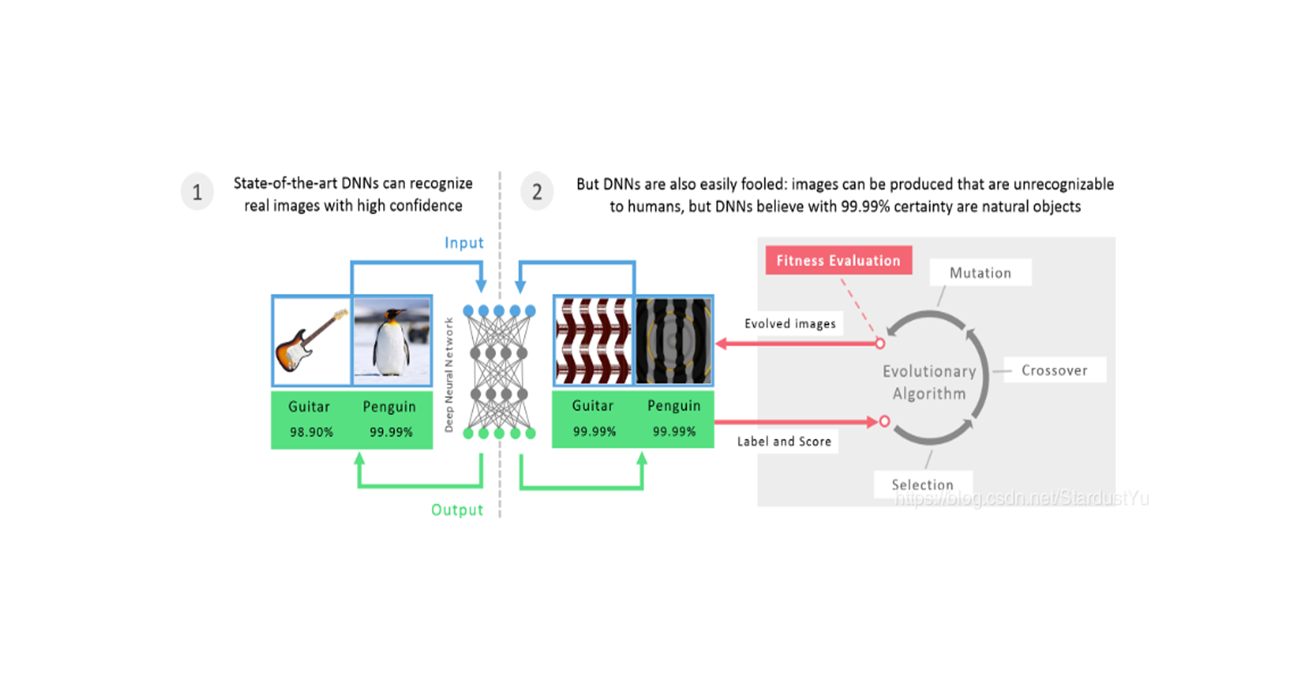
   先前对于生成对抗样本的工作主要关注点在于 使用错误类别label来设计优化方程，来得到对抗样本。该篇论文关注于 利用DNN内部网络层的respresentation来设计优化方程，进而得到对抗样本。对抗样本虽然与其原始图像相似，但是在网络内部表示上，却跟另一个类别不同的图像相似，并且与输入几乎没有任何明显的相似性。

三、论文内容总结

• 提出了一种新的生成对抗样本的方法。该方法具有原始图像和目标图像，生成的对抗样本虽然与其原始图像相似，但是在网络内部表示上，却跟目标图像的内部表示相似。

$$\begin{split} I_{\alpha}=&arg\ min_I ||\phi_k(I) - \phi_k(I_g)||_2^2\\ &\quad s.t. ||I- I_s||_{\infty} < \delta\\ \end{split}$$

• 通过几种距离的量化方法，得到了对抗样本所得到的内部representation与目标图像所得到的内部representation的相似度。得出结论，当$ \delta$ 越大，对抗样本越接近目标图像。
• 通过几种量化方法，得到结论对抗样本$ \alpha$ 的representation属于正常图片的representation。（数学要求较高，未看懂）
• 通过对随机初始化的网络进行实验，得到feature opt对抗样本可能是网络结构的一个特性。

附：如需继续学习对抗样本其他内容，请查阅对抗样本学习目录

四、论文主要内容

1. Introduction

   对抗样本存在的意义是很重要的，不仅是因为它揭示了在学习到的representation和分类器上的脆弱性，而且它们提供了探索有关dnn本质的基本问题的机会，例如它们是网络结构本身固有的还是学习模型固有的；这种对抗性的图像可以用来改进学习算法，从而产生更好的泛化和鲁棒性。

   之前的工作可以被称为label adversaries，其主要关注于分类标签错误。该论文的方法不仅仅使用了label，而且利用了他们的内在表示来生成对抗样本，称之为feature adversaries。

   给定原图像，目标图像和一个训练好的DNN网络，我们尝试找到一个小的扰动加在原图像上，使其生成的内在representation与目标图像的内在representation相似。我们已经证明，我们几乎可以把一个图像攻击成任意一个图像。这一现象引起了对DNN的representation的质疑。

2. Related Work

   介绍了之前的工作

3. Adversarial Image Generation

   记$ I_s$ 和$ I_g$ 分别表示原图像和目标图像，$ \phi_k$ 表示一个图像到网络第k层representation的映射。我们的目标就是找到一个新的图像$ I_{\alpha}$ ，使得$ \phi_k(I_{\alpha})$ 与$ \phi_k(I_g)$ 的欧氏距离尽可能小，且$ I_{\alpha}$ 要与$ I_s$ 尽可能相似。即：

$$\begin{split} I_{\alpha}=&arg\ min_I ||\phi_k(I) - \phi_k(I_g)||_2^2\\ &\quad s.t. ||I- I_s||_{\infty} < \delta\\ \end{split}$$

   其限制条件，使用了$ \infty$ 范数，限制了每个像素点的最大变化值为$ \delta$ 。$ L_{\infty}$ 范数对人类视觉辨认来说并不是最优的，其差于SSIM，但是优于$ L_2$ 范数。

   我们固定$ \delta = 10$ （像素范围为0~255）。而且，我们有时会把靠近输入的低层的$ \delta$ 设高一些，因为随着网络层数的增加，差别就会越来越小。注意，这里的优化式子只采用了一层网络的representation。

   我们使用了L-BFGS-B来对box constraint的限制条件进行优化。

   尽管在我们优化的过程中并没有使用标签，但是我们发现，几乎所有修改后的图像的标签跟目标图像的标签一致。作者对100个图像对进行了实验，发现95%的图像被分类成目标图像的标签。

   同时，这样生成的对抗样本可以泛化到其他网络中，100个对抗样本，有54%的攻击成功。

   接下来，我们就要去探索内部representation，它是更像原图像，还是更像目标图像，还是两者的结合呢？一种去探索内部representation的方式就是反转映射，也就是根据特定层的representation重建输入图像，采用的方法是论文Mahendran, A and Vedaldi, A. Understanding deep image representations by inverting them. In IEEE CVPR (arXiv:1412.0035), 2014. 3,提到的。

   首先，作者得到了原始图像、目标图像、以及将Caffenet的FC7、P5、C3层分别作为优化目标而得到的对抗样本。

  

   之后利用C3、P5、FC7的representation进行重建输入图像，得到的图像如下。

   从重建得到的图像我们可以得知，层数越低，其重建得到的图像越像原图像，层数越高，其重建得到的图像越像目标图像。这也说明，人类感知与DNN的表示是不一样的。

4. Experimental Evaluation

   作者提出了两个问题，对抗样本得到的DNN的内部representation与对应的目标图像的representation的相似程度如何？从某些角度来看，这些representation是否是不自然的？作者使用Caffenet与ImageNet数据集来进行实验。

4.1 Similarity To The Guide Representation

   提出了一种量化测量方式，来测量原图像、目标图像以及对抗样本之间的相似度。

   当使用FC7进行优化时，我们使用了20000个source-guide对来进行测试，这些图片来自于ImageNet的ILSVRC的训练集、测试集、验证集甚至还有Wikipedia的一些图片。当使用更高维度的层（例如P5）进行优化时，我们使用了一个较小的数据集，采用了2000个source-guide对。我们采用$ s,g,\alpha$ 分别表示原始图像，目标图像以及对抗样本。

欧氏距离

   作者记录了对抗样本$ \alpha$ 和目标图像$ g$ 的距离$ d(\alpha,g)$ 与原始图像$ s$ 和目标图像$ g$ 的距离$ d(s,g)$ 的比值。比值小于0.5表示，$ \alpha$ 更像目标图像$ g$ 。并绘制数据集上这些比值的直方图。经过实验发现，当$ \delta$ 越大，$ \alpha$ 越像$ g$ 。见图像(a)。

   作者计算了一个这样的距离，得到ILSVRC训练集中所有与$ g$ 同label的图像，得到该图像在FC7层representation上的最近邻的图像，计算该图像与该最近邻图像的距离，在整个训练集上取平均，记为$ \bar{d_1}(g)$ 。记录了对抗样本$ \alpha$ 与目标图像$ g$ 的距离$ d(\alpha,g)$ 与$ \bar{d_1}(g)$ 的比值。比值小于1表示，$ \alpha$ 相比于数据集上的最近邻，距离$ g$ 更近。绘制在测试集上这些比值的直方图。经过实验发现，当$ \delta$ 越大，$ \alpha$ 与$ g$ 越近，见图像(b)。

   作者计算了一个这样的距离，得到ILSVRC训练集中所有与$ s$ 同label的图像，计算$ s$ 与任意一个图像在FC7上representation的距离的平均置$ \bar{d}(s)$ ，计算了$ \alpha$ 与$ s$ 在FC7层上representation的距离$ d(\alpha,s)$ 与$ \bar{d}(s)$ 的比值。比值大于1表示，$ \alpha$ 大于$ s$ 类内的平均距离。绘制测试集上这些比值的直方图。经过实验发现，当$ \delta$ 越大，$ \alpha$ 离$ s$ 越远。见图像(c)。

Intersection and Average Distance to Nearest Neighbors 最近邻居的交集 和 到最近邻居的平均距离

   观察图像的最近邻提供了另一种相似性度量。当点的密度通过特征空间发生显著变化时，该方法非常有用，在这种情况下，欧氏距离可能没有意义。为此，我们通过对近邻的排名统计来量化相似度。

   我们取到一个点到K个近邻的平均距离作为该点的分数。然后，我们将该点与训练集中同一标签类的所有其他点进行排名。因此，排名是平均距离的非参数变换，但与距离单位无关。

   我们记某一个点$ x$ 的分数（即到K近邻的平均距离）为$ r_K(x)$ ，我们使用$ K=3$ ，而且在计算对抗样本$ \alpha$ 的K近邻时，我们会排除原始图像$ g$ 。我们可以记录对抗样本$ \alpha$ 与目标图像$ g$ 的rank差$ \Delta r_3(\alpha,g) = r_3(\alpha)-r_3(g)$ ，如果$ \alpha$ 越靠近$ g$ 那么$ \Delta r_3(\alpha,g)$ 就会越小，且$ \alpha$ 与$ g$ 的K近邻集合将会相交。

   下面的表记录了对100个source-guide对进行实验时，得到的K近邻集合相交个数在3，和2的个数，以及$ \Delta r_3$ 的值。

4.2 Similarity To Natural Representations

   我们已经知道了对抗样本的内在representation时什么样子的了，那么正常图像的内在representation该是什么类型的呢？也就是说，在$ g$ 的附近，$ \alpha$ 是一个内点吗，它的特征和附近的其他点一样？

   作者通过计算两个neighborhood属性来回答。1）一种概率参数测度，给出一点相对于g处局部流形的对数似然性；2）基于高维离群点检测方法的几何非参数测度。

   我们记$ \mathcal{N}_K(x)$ 表示$ x$ 点的K近邻集合，记$ N_{ref}$ 是一组参考点，由$ \mathcal{N}_{20}(g)$ 随机选取15个点得到，记$ N_c$ 表示剩下的点，即$ N_c = \mathcal{N}_{20}(g) \backslash N_{ref}$ 。令$ N_f = \mathcal{N}_{50}(g) \backslash \mathcal{N}_{40}(g)$ 。参考集$ N_{ref}$ 用于测量函数的构建， 通过下面两种测量方法对$ \alpha,N_c,N_f$ （相对于$ g$ ）进行评分。

   在高维特征空间来测量两个点的相似度时，利用欧氏距离的意义不大，因此我们采用了余弦距离来找到K近邻。

Manifold Tangent Space 流形切线空间

   我们建立了一个以$ g$ 为中心的概率主成分分析（PPCA）的概率子空间模型，并将$ \alpha$ 的似然性与其它点进行了比较。更准确地说，PPCA应用于$ N_{ref}$ ，其主空间是一个正割平面，其法向与正切平面大致相同，但由于流形的曲率，所以一般不通过$ g$ 。我们通过移动平面使其通过g来修正这个小的偏移量；对于PPCA，这是通过将高维高斯的均值移动到$ g$ 来实现的。然后，我们评估模型下点的对数似然，相对于$ g$ 的对数似然，表示为$ \Delta L(·，g)=L(·)–L(g)$ 。我们对大量的source-guide对重复此测量，并将$ \alpha$ 的$ \Delta L$ 分布与$ N_c$ 和$ N_f$ 中的点进行比较。（太数学了，这边没看懂）

   我们发现，目标图片$ g$ 虽然来源不同（训练集、验证集），但是得到的曲线相似。这表明我们的方法得到的对抗样本是representation的内在属性，而并不是因为模型的泛化性。

Angular Consistency Measure 角一致性测量

   如果$ g$ 的近邻点在高维特征空间中是稀疏的，或者流形具有较高的曲率，则线性高斯模型将是一个不合适的模型。因此，我们考虑一种不依赖流形假设的方法来检验$ \alpha$ 是否是$ g$ 附近的内环。我们在$ g$ 附近取一组参考点$ N_{ref}$ ，测量$ g$ 到每个点的方向。然后，我们将来自$ g$ 的方向与来自$ \alpha$ 和其他邻近点的方向进行比较，例如在$ N_c$ 或$ N_f$ 中，以查看$ \alpha$ 在角度一致性方面是否与$ g$ 周围的其他点相似。与局部流形内的点相比，远离流形的点与流形内其他点的方向范围更窄。具体来说，给定参考集$ N_{ref}$ ，具有基数K，$ z$ 是$ \alpha$ ，或者是$ N_c$ 或$ N_f$ 的一个点，我们的角一致性度量定义为：

$$\Omega(z,g) = \frac{1}{k}\sum_{x_i \in N_{ref} } \frac{<x_i-z,x_i-g>}{||x_i-z||\ ||x_i - g||}$$

   上图的图(c)和图(f) 是显示了$ \Omega(\alpha,g)$ 相比于$ \Omega(n_c,g)$ 以及$ \Omega(n_f,g)$ 的直方图，其中$ n_c \in N_c,n_f \in N_f$ 。注意：角度一致性的最大值为1，值越大表明越像$ g$ 。

   除了标度和上界的差异之外，角一致性图4（c）和4（f）与图4前两列中的似然比较图惊人地相似，支持对抗样本$ \alpha$ 的representation属于正常图片的representation。

4.3 Comparisons And Analysis

   在这一节主要是将我们的方法与之前的方法进行比较，同时研究了Goodfellow提出的对抗样本出现的原因是因为模型的线性特性引起的 的假设。我们将我们的方法称之为feature adversaries，优化方法称为feature-opt。将之前的通过误分类的方法称之为label adcersaries，其对应的优化方法称之为label opt。

Comparison to label-opt

   1. 使用了4.1节提到的度量方法，发现经过feature opt得到的$ \alpha$ ，其rank与$ n_1(\alpha)$ 有强烈的相关性，而用label opt得到的$ \alpha$ 却没有这样的相关性。

   2. 使用了4.2提到的流行PPCA方法，与下图中feature opt得到的标准的似然峰值直方图不同，图(b)表明，label opt得到的对抗样本并不能被$ \alpha$ 的最近邻很好的表示

   3.基于不同的对抗样本生成方法（使用不同的DNN层进行优化）， 作者分析了在不同DNN层上的稀疏性，我们都知道ReLU激活单元可以生成稀疏的激励，因此，如果在添加对抗扰动后，系数程度增加了，这也就说明对抗样本使用了新的路径来控制最终的representation。我们也观察了原图像和对抗样本中，有多少单元是激活状态？通过计算激活单元的联合I/U上的交集，我们可以得出其激活状态的差别。如果I/U值很高，说明两者共享大部分相同的激活单元，如果I/U值很低，说明对抗样本关闭了一些激活单元路径，打开了一些新的路径。

   下图是实验结果，$ \Delta S$ 表示的是，在给定的层上，两种类型的攻击方法上的非零激活单元的比例的差异。根据这个我们可以看出，除了FC7，其他的结果差异都很大。（我看不出来是啥意思，很迷）

Testing The Linearity Hypothesis for feature-opt 测试 feature opt的线性假设

   GoodFeelow表明，对抗样本的存在是网络过于线性化的结果。如果这种线性假设适用于我们这类方法，则应该可以将源图像周围的DNN线性化，然后通过优化获得类似的对抗样本。

   我们令$ J_x = J(\phi(I_s))$ ，表示内部层的Jacobian矩阵（相对于原图像输入），那么线性假设可以描述为$ \phi(I) \approx \phi(I_s)+J_s^T(I-I_s)$ ，因此我们的目标函数变为$ ||\phi(I_s)+J_s^T(I-I_s)-\phi(I_g)||_2^2$ 。我们把这类攻击称之为feature-linear。

   实验结果如下图所示，可以看出，这些对抗样本并没有离目标图像很近，他们的$ d(\alpha,g)/d(s,g)$ 超过80%，而feature opt得到的距离小于50%。注意，与feature opt不同，feature linear的目标不能保证当$ \delta$ 的约束放松时距离的减少。这些结果表明线性假设不能解释feature opt对抗样本的存在。

Networks with Random Weights

   我们进一步的探索，feature opt对抗样本的存在是因为学习算法、训练集还是深度网络的结构。为此，我们随机的正交初始化Caffenet的权重，然后进行优化得到对抗样本，观察在4.1节提到的距离比值。有趣的是，我们发现FC7和Norm 2的距离比与上图Fig 5的样子类似。这表明，feature opt对抗样本可能是网络结构的一个特性。

5. Discussion

   引入了一种新的生成对抗样本的方法，其得到的对抗样本虽然与其原始图像相似，但是在网络内部表示上，却跟另一个类别不同的图像相似，并且与输入几乎没有任何明显的相似性。

   我们发现线性假设并不能对feature opt对抗样本进行很好的解释，似乎这些对抗性图像的存在并不是建立在自然图像本身训练的网络上。而可能是网络结构的一个特性。然而，还需要进一步的实验和分析来确定人类和DNN图像表示之间存在差异的真正根本原因。

   另一个未来的方向是探索我们在优化featrue opt对抗样本时观察到的失败案例。这些失败表明，我们的对抗现象可能是由于网络深度、接受野大小或使用的自然图像类别等因素造成的。由于我们在这里的目的是分析知名网络的表现形式，因此我们将这些因素的探索留给未来的工作。另一个有趣的问题是，是否可以训练现有的判别模型来检测feature 对抗样本。由于训练这样的模型需要一个不同的和相对较大的对抗性图像数据集，我们也把这留给未来的工作。