对抗样本（十五）Natural GAN

一、论文相关信息

  1.论文题目

     Generating natural adversarial examples

  2.论文时间

    2017年

  3.论文文献

     https://arxiv.org/abs/1710.11342

  4.论文引用

     Zhao Z, Dua D, Singh S. Generating natural adversarial examples[J]. arXiv preprint arXiv:1710.11342, 2017.

二、论文背景及简介

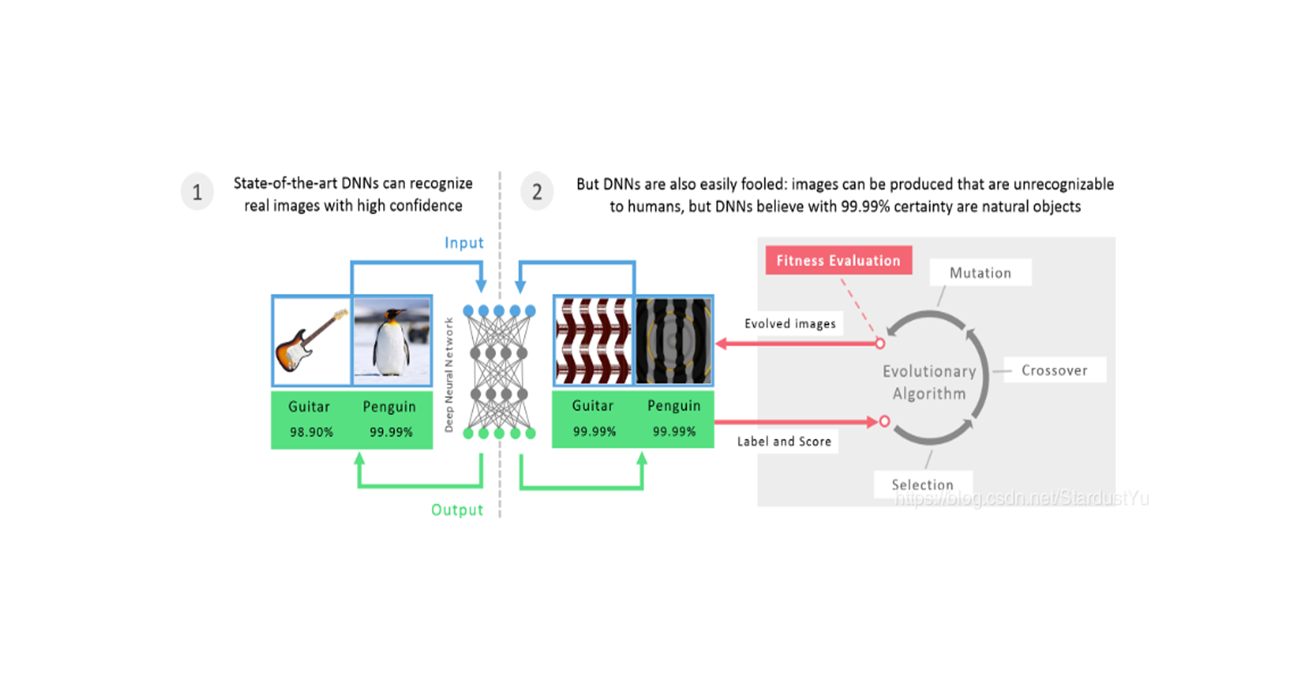
   目前，对抗扰动都很不自然、没有语义意义、无法应用到复杂的领域，例如语言。本文利用生成对抗网络的最新进展，提出了一种在数据流形上生成自然易读的对抗样本的方法，该方法通过搜索密集连续数据表示的语义空间来生成自然易读的对抗实例。

三、论文内容总结

• 借用GAN，生成更加自然的对抗样本

附：如需继续学习对抗样本其他内容，请查阅对抗样本学习目录

四、论文主要内容

1. Introduction

尽管对抗样本揭露了ML存在的盲点问题，但是这些对抗样本并不会在自然情况下产生，在模型部署时，很难遇到这样的样本。因此，很难深入了解黑盒分类中的基本决策行为：为什么对于对抗样本而言决策是不同的？为了阻止这一行为，我们改变了什么？分类器对数据的自然变化是不是鲁棒的？另外，在输入空间和语义空间存在不匹配的问题，我们对输入空间做一些无意义的变化比如光照强度的变化，却会导致其在语义空间发生大的变化。

最直接的想法就是对于攻击者而言，在一个密集的连续的数据表示空间中搜索，而不是在直接在数据空间中搜索。我们使用GAN将正态分布的固定长度向量映射到数据样本。在给定输入实例的情况下，我们通过在递归收紧的范围内采样，在潜在空间中的对应表示附近搜索对抗样本。

2. Framework For Generating Natural Adversaries

   给定黑盒分类器$ f$ ，一组未标签数据$ X$ ，目标是为一个给定的样本$ x$ 生成对抗样本$ x^$ ，注意这里的$ x$ 不一定在$ X$ 内，但一定与$ X$ 来自于同样的数据分布$ P_x$ 。我们想要**基于数据分布$ P_x$ 的流行上，让$ x^$ 离$ x$ 最近**，而不是在原始的数据表示上。

   而距离的评判并不是在原始的输入空间，我们将会在一个对应的密集表示空间$ z$ 中来寻找$ x^$ 。也就是说，**我们首先会有一个现在的密集向量空间，其与数据分布$ P_x$ 对应，我们将原始样本映射到空间中，在其附近找到对抗样本$ z^$ ，使用GAN映射回原始空间，得到最终的对抗样本$ x^$ 。* 通过这种方法得到的对抗样本会更加的有效（图片更加清晰，句子更有语法），在于以上更接近于原始输入。

2.1 GAN介绍

   给定分类其$ f$ ，一组unlabel数据$ X$ ，我们的目标是生成一个对抗样本$ x^$ 使得$ f(x^) \ne f(x)$ ，$ x$ 并不一定是$ X$ 内的数据，但是，他们一定是服从同样的数据分布$ \mathcal{P}_x$ ，我们要是$ x^$ 在这个数据分布上，尽可能与$ x$ 相靠近，而并不是让$ x^$ 的representaion与$ x$ 的representaion靠近。

   我们的方法是，是首先在服从分布$ \mathcal{P}_x$ 的$ z$ 空间中找到一个对抗样本$ z^ $ ，然后使用GAN，将$ z^$ 映射回$ x^*$ ，我们发现，这样的对抗样本更加真实，与原始输入语义更接近。

2.2 Natural Adversaries

   什么是真实的对抗样本？

   我们首先使用数据集$ X$ 训练一个WGAN，在WGAN中，可以把一个随机的向量$ z \in \mathbb{R}^d$ 映射到样本空间$ X$ 中的$ x$ 上。另外，我们又训练了一个反转器$ \mathcal{I}_{\gamma}$ ，其可以将样本$ x$ ，映射回向量空间$ z’$ ，如下图所示：

   我们，通过最小化$ x$ 的重建损失$ \mathcal{C}_{w}$ ，以及divergence$ \mathcal{L}$ 来训练分类器。

   于是，我们定义，Natural Adversarials是：

$$x^* = \mathcal{G}_{\theta}(z^*)\ where\ z^* = \arg \min_{\tilde{z}}||\tilde{z} - \mathcal{I}_{\gamma}(x)||\ s.t. f(\mathcal{G}_{\theta}(\tilde{z})) \ne f(x)$$

   使用这种方法，我们并不是扰动样本$ x$ ，而是扰动$ z’ = \mathcal{I}_{\gamma}(x)$ ，然后使用生成器来判断是否一个扰动$ \tilde{z}$ 欺骗了分类器。其迭代过程如下图所示：

   对于divergence $ \mathcal{L}$ ，我们在图像领域使用$ \lambda = 0.1$ 的$ L_2$ 距离，在文本数据中采用$ \lambda = 1$ 的Jensen-Shannon距离。

2.3 Search Algorithms

   作者提出了两种方法在$ z’$ 得附近寻找扰动$ \tilde{z}$ 。

① 随机迭代寻找

   我们会递增的扩大寻找范围$ \Delta r$ ，在该范围内，随机采样$ N$ 个，知道我们生成了对抗样本$ \tilde{x}$ 。在这些对抗样本中，我们会选择最接近$ z^*$ 得那一个作为输出。

② 混合收缩寻找

   为了提高第一种算法的效果，提出了一种从粗到细得策略。我们首先在较宽的搜索范围内搜索，然后在二等分中以更密集的抽样递归地收缩搜索范围的上限。其速度大概是第一种方法得四倍。

3.Illustrative Examples

3.1 Generating Image Adversaries

   采用数据集MNIST和LSUN，使用参数$ \Delta r=0.01,N=5000$

3.1.1 Handwritten Digits

   在MNIST数据集上，训练了一个$ z\in \mathbb{IR}^{64}$ 得WGAN。生成器由转置卷积组成，判别器由卷积层组成，在判别器的最后一层隐藏层上添加全连接层构建逆变器。

   采用的目标分类器有两个，一个是Random Forest，五棵树，测试准确率90.45%；一个是LeNet，测试准确率98.71%。

3.1.2 Church vs Tower

   在LSUN中取126227张church和tower的图片，resize到64x64。训练了一个$ z\in \mathbb{IR}^{128}$ 的WGAN，生成器和判别器采用了残差网络。采用MLP分类器，在这两类的测试准确率为71.3%。

3.2 Generating Text Adversaries

   由于文本的离散性，生成语法和语言上连贯的对抗文本是一项具有挑战性的任务：我们不可能添加不可察觉的噪音，而且对$ x$ 的大多数的更改可能会产生语法不通的文本。

   我们使用一个对抗性正则化的自动编码器（ARAE），来将离散的文本编码成连续的编码。ARAE会使用一个LSTM编码器将一个句子编码成连续的编码（向量），然后在这些编码上进行对抗训练来捕获数据分布。之后，我们引入了Inverter，将这些编码映射到高斯空间$ z \in \mathbb{R}^{100}$ 。

   作者使用了四层的CNN用作编码器，使用了LSTM作为解码器。然后训练了两个MLP模型，分别用作生成器和inverter，来学习noise和连续编码的映射关系。

4.Experiments

4.1 Robustness of Black-box Classifier

   将我们的方法用到各种各样的黑盒分类其中，来评测这些模型的鲁棒性。一般来说，更精确的分类器需要对样本进行更多的改变才能改变其预测值。

4.2 Human Evaluation

   作者进行了调查，询问生成的对抗样本的自然程度和与原始样本的相似程度

5. Related Work

   略

6. Discussion And Future Work

• 提高GAN模型的能力，找到能处理文本离散问题的模型

7. Conclusions

   本文，提出了一个生成更加自然的对抗样本的方法，将这种方法应用到了视觉和文本领域。