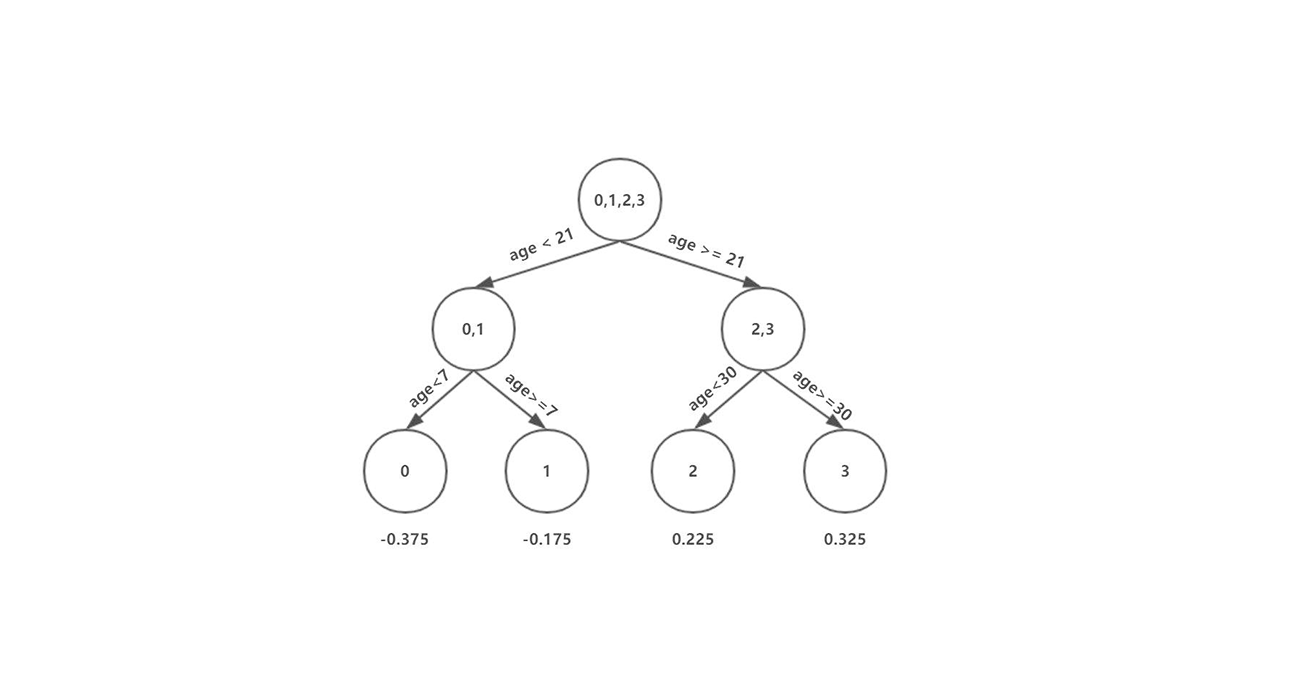
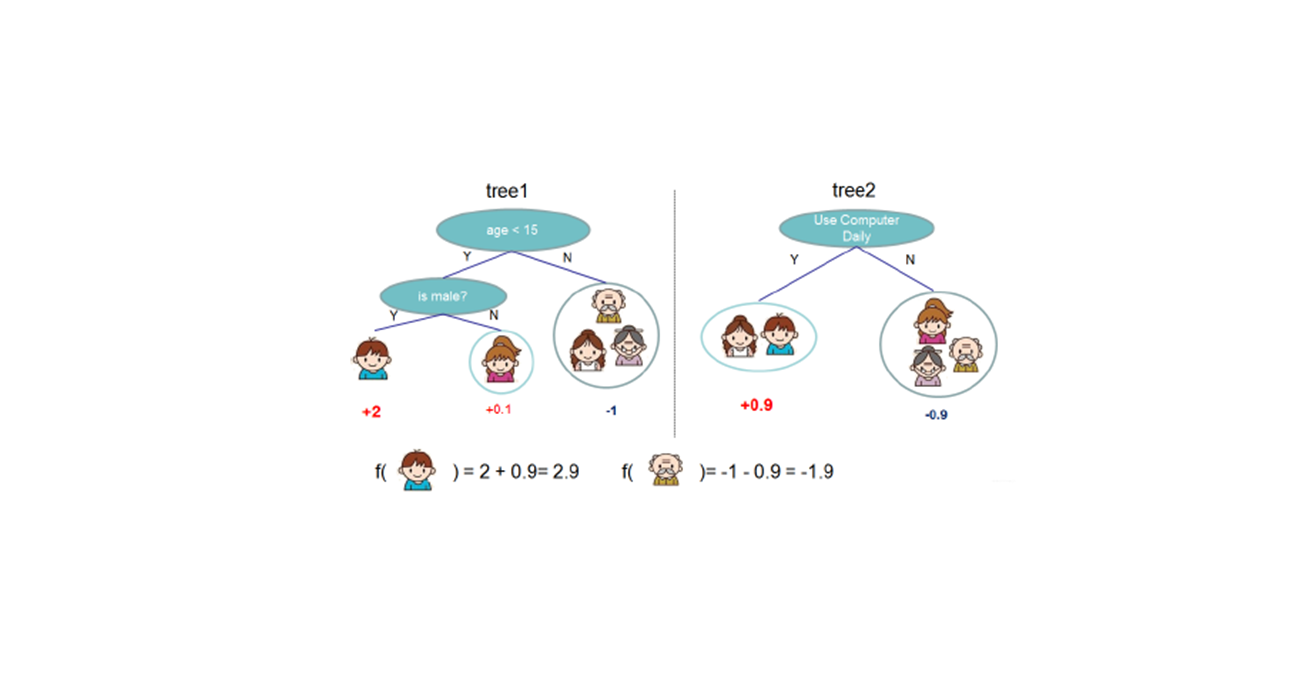
一、模型介绍
AdaBoost方法的自适应在于:前一个分类器分错的样本会被用来训练下一个分类器。AdaBoost方法是一种迭代算法,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率。每一个训练样本都被赋予一个权重,表明它被某个分类器选入训练集的概率。如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它被选中的概率就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。通过这样的方式,AdaBoost方法能“聚焦于”那些较难分(更富信息)的样本上。虽然AdaBoost方法对于噪声数据和异常数据很敏感。但相对于大多数其它学习算法而言,却又不会很容易出现过拟合现象。
AdaBoost是一种”加性模型”,即基学习器的线性组合:
整体要做的事情,就是最小化指数损失函数:
1、训练过程
最初,训练集会有一个初始的样本权值分布(平均分布),基于训练集$ D$ 与该分布$ D_t$ 训练一个基学习器$ h_t$ ,估计$ h_t$ 的分类误差,根据误差确定分类器$ h_t$的权重,根据误差等信息重新确定样本的权值分布$ D_{t+1}$ (为分类错误的样本增加权重),伪代码如下图所示:

接下来的部分是伪代码中的公式推导,如果不想看的,可直接跳过这些,直接到样本分布&重采样后再看。
2、损失函数的确定
我们为什么要用指数损失函数呢?下面来看,当我们最小化指数损失函数是,我们是否能够得到最优的分类器$ H(x)$ 。
计算损失函数对$ H(x)$ 的偏导:
令偏导数为0,我们可得:
看一下,我们得到的$ H(x)$ 是都是最优的,是否满足分类要求?
我们可以知道,$ sign(H(x))$ 达到了贝叶斯最优错误率,也就是说该损失函数是可以的。
3、分类器权重$ \alpha_t$ 的确定
我们基于分布$ D_t$ 训练出来了一个分类器$ h_t$ ,那么我们该给他们分配怎样的权重,才能最小化损失函数呢?
观察$ \alpha_th_t$ 的损失函数形式:
其中$ \epsilon_t = P_{x\sim D_t}(h_t(x)\ne f(x))$ ,$ Ⅱ(·)$ 表示概率,计算损失函数对$ \alpha_t$ 的导数:
令导数为0,我们可得:
4、样本权重分布的确定
AdaBoost算法,在获得$ H_{t-1}$ 之后,样本分布将进行调整,使下一轮的基学习器$ h_t$ 能纠正$ H_{t-1}$ 的一些错误,理想的$ h_t$ 能纠正$ H_{t-1}$ 的全部错误,即最小化:
我们对$ e^{-f(x)h_t(x)}$ 进行泰勒展开,并考虑到$ f^2(x)=h_t^2(x)=1$ ,我们得到:
因此,我们要得到的理想的基学习器是:
在第$ t$ 次迭代时,$ H_{t-1}(x)$ 是已知的,因此可以将其当作常数,则上式转换为:
我们可以令$ D_t$ 表示为下面这个分布:
根据数学期望的定义,这等价于:
因为$ f(x),h(x) \in {-1,1}$ ,那么:
那么,我们得到的理想的学习器,就是:
因此,在分布$ D_t$ 下,我们的弱分类器就能够得到最优值,根据残差逼近的思想,对分布进行迭代式的逼近,得到:
5、样本分布&重采样
Boosting算法要求基学习器能对特定的数据分布进行学习,这可通过“重赋权法”实施,即在训练过程的每一轮中,根据样本分布为每个训练样本重新赋予一个权重。
对无法接受带权样本的基学习器算法,则可通过“重采样法”进行处理,即在每一轮学习中,根据样本分布对训练集重新进行采样,再用重采样而得到的样本集对基学习器进行训练。
6、AdaBoost示例

我们可以将基分类器设为线性分类器,那么迭代过程中的分类效果图如上图所示。
7、AdaBoost 总结
- 简单,不用做特征筛选
- 不用担心overfitting!
- adaboost是一种有很高精度的分类器
- 只适用于二分类任务
参考链接
- AdaBoost算法详解
- 周志华老师的《机器学习》