一、模型介绍

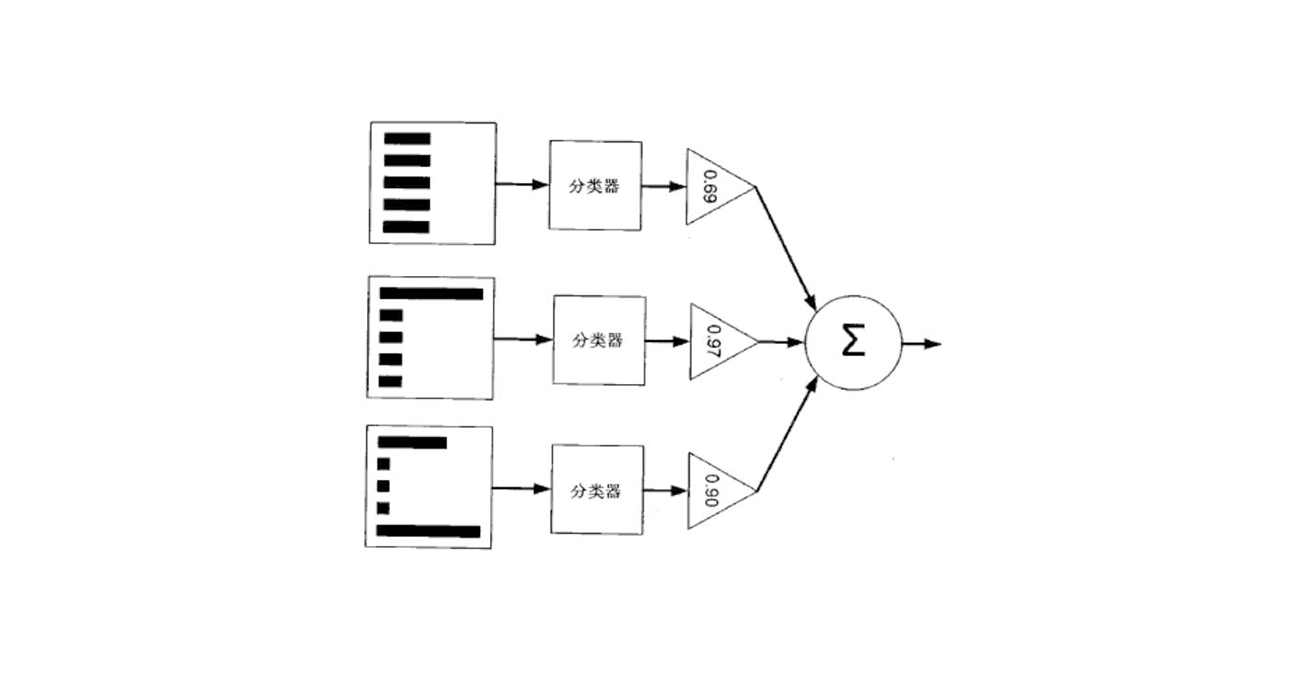
XGBoost的全称是 eXtremeGradient Boosting，2014年2月诞生的专注于梯度提升算法的机器学习函数库，作者为华盛顿大学研究机器学习的大牛——陈天奇。他在研究中深深的体会到现有库的计算速度和精度问题，为此而着手搭建完成 xgboost 项目。xgboost问世后，因其优良的学习效果以及高效的训练速度而获得广泛的关注，并在各种算法大赛上大放光彩。

在我们使用GDBT时，我们采用多次小步的迭代方式来拟合我们的集成模型，GDBT只利用了训练集的一阶信息，这使得我们拟合的速度比较慢，这就造成了我们在训练时可能会生成大量的树模型。为了解决这个问题，XGBoost，采用了训练集的二阶信息，加快了拟合速度，同时修改了在属性划分时的规则，提高了精度。

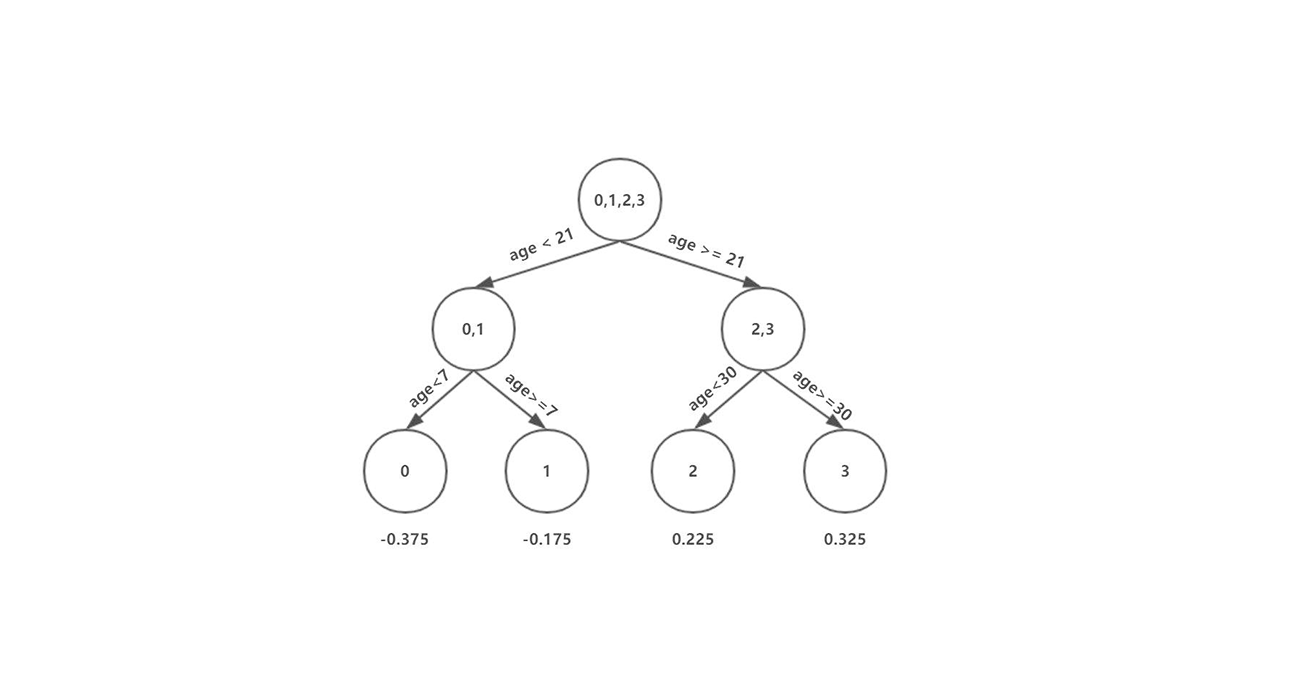
XGBoost的基学习器可以是任意的学习器，比如LR、决策树等，在这里以决策树为例进行讲解。XGBoost可以表示为决策树的加法模型：

$f_M(x) = \sum_{m=1}^MT(x;\Theta_m)$

其中，$ T(x;\Theta_m)$ 表示第m颗决策树，$ \Theta_m$ 表示决策树的参数，$ M$ 表示树的个数。

XGBoost的损失函数可以是任意的自定义的损失函数，这里以平方误差为例：

$L(y,f(x)) = (y-f(x))^2$

XGBoost的目标函数中包含了其损失函数以及正则化项，其中n表示数据集的数量，t表示当前的迭代标号：

$Obj^{(t)} = \sum_{i=1}^nL(y_i,\hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i)$

1、训练过程

在XGBoost的训练过程中，我们在每次的迭代过程中，我们依然是构建一个新的树来拟合数据的残差$ r=y-f_{m-1}(x)$ ，其算法叙述如下：

首先初始化$ f_0(x)=0$ ，初始化第一个残差数据集$ r_i=y_i-f_0(x_i)$ （原数据集），根据原数据以及目标函数，采用XGBoost特有的分割节点的策略来建立一颗树$ T(x;\Theta_0)$ ，根据树得到的结果，再次计算残差，将这次得到的残差作为下一颗树的数据集，得到下一颗树$ T(x;\Theta_m)$ ，并且更新$ f_m(x) = f_{m-1}(x)+T(x;\Theta_m)$ ，不断地迭代，我们就能够得到最终的集成模型：

根据上述的训练过程，我们不得不有一些疑问。我们怎样根据我们的目标函数来设计我们的分割策略呢？，我们怎样把XGBoost应用到其他模型上呢？，让我们按顺序来看一下下面的解析

2、目标函数的确定

我们已经知道，第t轮迭代的目标函数的固定形式为：

$Obj^{(t)} = \sum_{i=1}^nL(y_i,\hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i)$

对于第t轮迭代来说，前t-1轮的正则化项我们已经知道了，所以可对其修改为：

$Obj^{(t)} = \sum_{i=1}^nL(y_i,\hat{y}_i^{(t-1)}+f_t(x_i)) + \Omega(f_t)+constant$

我们可以把$ \hat{y_i}^t=\hat{y_i}^{(t-1)}+f_t(x_i)$ 当成自变量，对Loss函数进行泰勒展开：

$f(x+\triangle x) = f(x) + f'(x)\triangle x + \frac{1}{2}f''(x)\triangle x^2$

根据上面的式子，我们可以把$ L$ 看作$ f(x)$，$ \hat{y_i}^{(t-1)}$ 看作$ x$，$ f_t(x_i)$ 看作$ \triangle x$ ，对目标函数展开如下：

$Obj^{(t)} = \sum_{i=1}^n\{L(y_i,\hat{y}_i^{(t-1)})+\frac{\partial L}{\partial \hat{y}_i^{(t-1)}}f_t(x_i)+\frac{1}{2}\frac{\partial^2 L}{\partial^2 \hat{y}_i^{(t-1)}}f^2_t(x_i)\} + \Omega(f_t)+constant$

我们知道在第$ t$ 次迭代时，$ L(y_i,\hat{y}_i^{(t-1)})$ 已知，并记$ g_i = \partial L/\partial {\hat{y}_i^{(t-1)}}$ ，记$ h_i = \partial^2 L/\partial^2 {\hat{y}_i^{(t-1)}}$，则目标函数变为：

$Obj^{(t)} = \sum_{i=1}^n\{g_if_t(x_i)+\frac{1}{2}h_if^2_t(x_i)\} + \Omega(f_t)+constant$

我们再来看一下正则化项

对于决策树而言，我们可以定义正则化项为：

$\Omega(f_t) = \gamma ·T +\frac{1}{2}\lambda\sum_{j=1}^Tw_j^2$

其中，$ T$ 表示树的叶子节点的个数，$ w_j$ 表示该叶子节点的输出值，$ \gamma \lambda$ 为常数。计算结果如下面显示：

带入正则化项

对于每一个$ f_i^t(x)$ 来言，它一定会被分类到某个叶子节点$ q$ 中，我们定义$ I_j$ 为叶子节点$ j$ 上的样本集合：

$I_j = \{i|q(x_i)=j\}$

带入正则化项后，那么我们的目标函数变为：

$\begin{equation} \begin{split} Obj^{(t)} &\approx \sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if^2_t(x_i)] + \gamma ·T +\frac{1}{2}\lambda\sum_{j=1}^Tw_j^2\\ &=\sum_{j=1}^T[(\sum_{i \in I_j}g_i)w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)w^2_j] + \gamma ·T\\ \end{split} \end{equation}$

我们记$ G_j = \sum_{i \in I_j}g_i$ ，$ H_j=\sum_{i \in I_j}h_i$，那么目标函数变为：

$Obj^{(t)} = \sum_{j=1}^T[G_jw_j+\frac{1}{2}(H_j+\lambda)w^2_j] + \gamma ·T\\$

假设树的结构已经固定

假设我们已经知道了树的结构，也就是说$ q(x)$ 已知。

我们可以看到，我们的目标函数变成了一个二次函数，那么其最优点在：

$W^*_j = -\frac{G_j}{H_j+\lambda}$

将最优点带入目标函数，我们可得：

$Obj^{(t)} = -\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda} + \lambda T$

当我们已知了树的结构，其计算方法如下图所示：

也就是说，当我们知道了树的结构时，我们可以根据目标函数，确定叶子节点应该取什么值最优。

3、确定分类标准

我们上面分析了当我们知道树的结构时，我们如何得到叶子节点的最优值。但是在我们构建树的时候，我们并不知道树的结构。那么我们应该怎么办呢？

我们的目的是让目标函数最小，因此我们可以使用贪心算法，在每一次分割时，都让目标函数减小一点，即我们要选择一个特征和特征值，在分割后达到下面的条件：

$\begin{equation} \begin{split} Obj_{split}&=-\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}]+\lambda T_{split}\\ Obj_{unsplit}&=-\frac{1}{2}\frac{(G_L^2+G_R)^2}{H_L+H_R+\lambda}+\lambda T_{unsplit}\\ Gain&=Obj_{unsplit} - Obj_{split}\\ &=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L^2+G_R)^2}{H_L+H_R+\lambda}]-\lambda (T_{split}-T_{unsplit}) \end{split} \end{equation}$

即找到能使Gain最大的分裂点。

如何对特征和特征值进行搜索

我们有暴力的贪婪解法

对于每个节点，枚举所有的特征
对于每个特征，根据特征值对实例（样本）进行排序
在这个特征上，使用线性扫描决定哪个是最好的分裂点
在所有特征上采用最好分裂点的方案

上面的暴力解法的效率很慢，于是就有了查找分裂点的近似算法：
枚举所有的特征
对于每个特征，根据特征值对实例（样本）进行排序
计算特征的分布（直方图）
将特征值分为k个桶，每个桶在直方图中的面积（即样本数量）是一样的，候选切分点就是桶的边界点
遍历所有的候选切分点，找到最好的分裂点。

两种分桶方案：

在建树之前预先将数据进行全局（global）分桶，需要设置更小的分位数间隔，这里用 $ \epsilon$ 表示，3分位的分位数间隔就是 1/3，产生更多的桶，特征分裂查找基于候选点多，计算较慢，但只需在全局执行一次，全局分桶多次使用。
每次分裂重新局部（local）分桶，可以设置较大的 $ \epsilon$ ，产生更少的桶，每次特征分裂查找基于较少的候选点，计算速度快，但是需要每次节点分裂后重新执行，论文中说该方案更适合树深的场景。

在方案1中，一般设置$ \epsilon=0.05$

在方案2中，一般设置$ \epsilon=0.3$

二、模型分析

1、XGBoost 对 GBDT 实现的不同之处

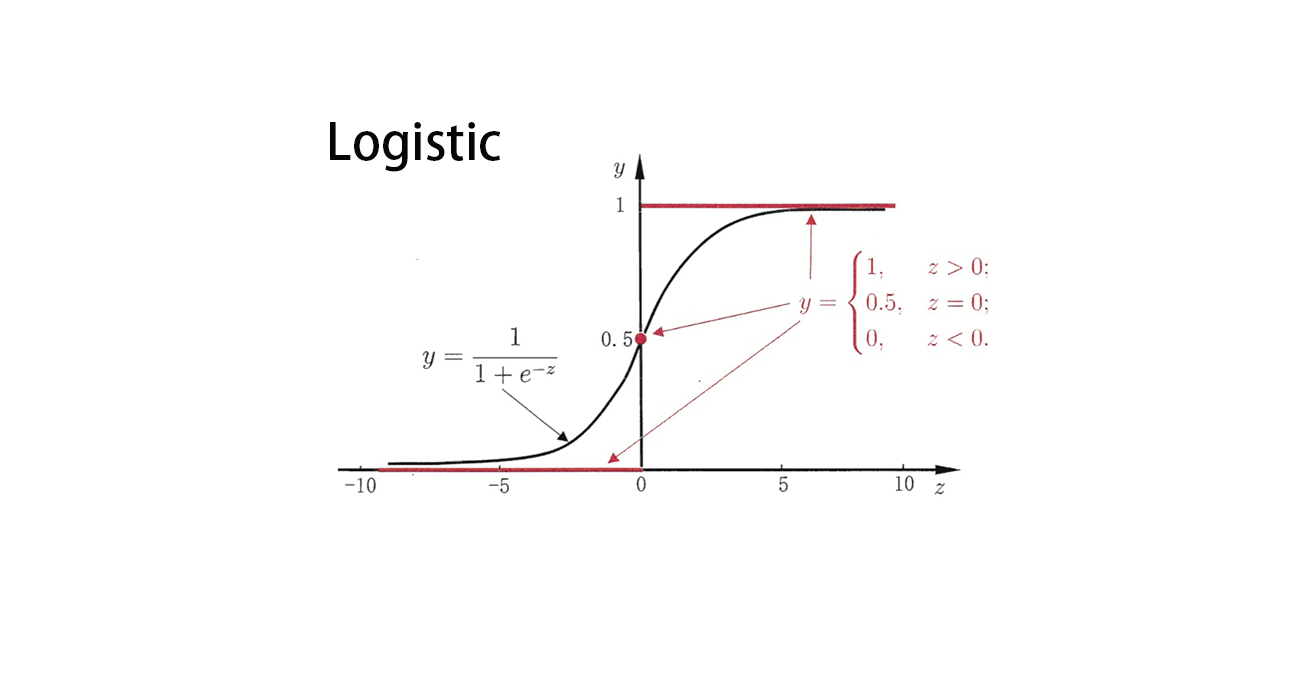
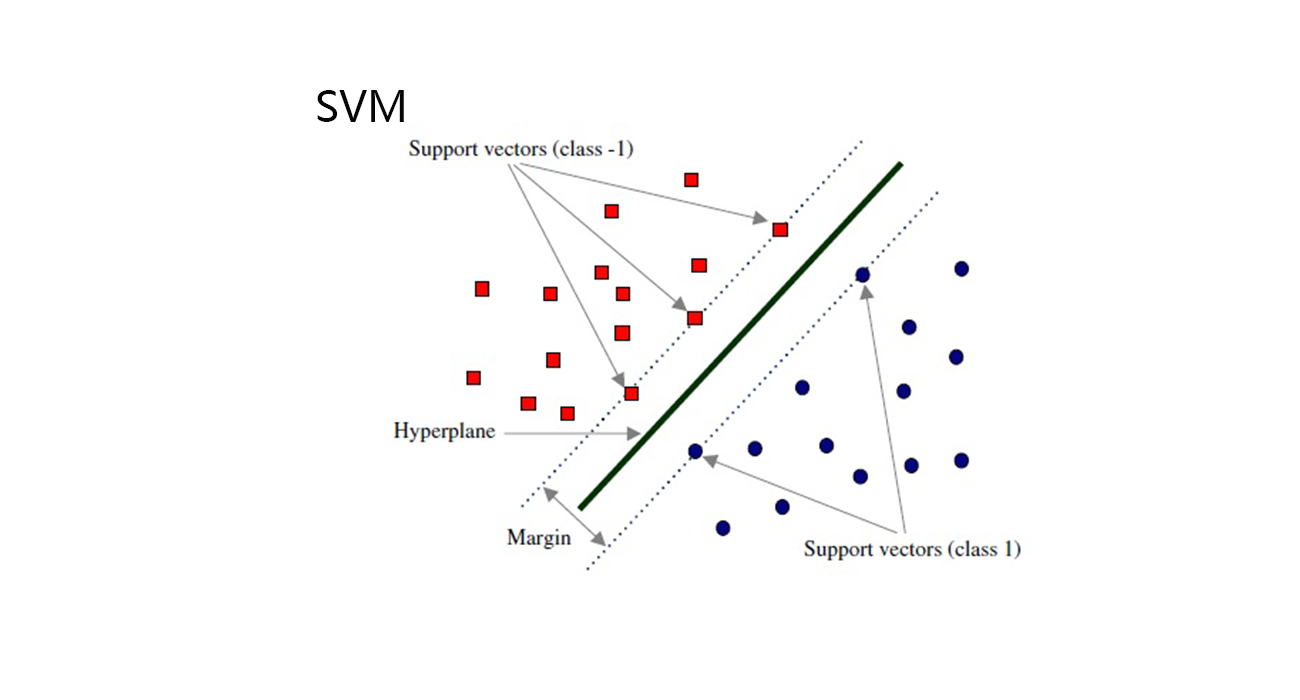
传统GBDT以CART作为基分类器，xgboost支持多种基础分类器。比如，线性分类器，这个时候xgboost相当于带 L1 和 L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。
传统GBDT在优化时只用到一阶导数信息，xgboost则对损失函数函数进行了二阶泰勒展开，同时用到了一阶和二阶导数，这样相对会精确地代表损失函数的值。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导，详细参照官网API。
xgboost在代价函数里加入了显式的正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和，防止过拟合，这也是xgboost优于传统GBDT的一个特性。正则化的两个部分，都是为了防止过拟合，剪枝是都有的，叶子结点输出L2平滑是新增的。
从最优化角度来看：GBDT采用的是数值优化的思维，用的最速下降法去求解Loss Function的最优解，其中CART决策树去拟合负梯度，用牛顿法求步长。XGBoost用的是解析的思维，对Loss Function展开到尔杰金斯，求得解析解，用解析解作为Gain来建立决策树，使得Loss Function最优