深度学习知识系列(二) 各种卷积形式

一、卷积的本质

    首先，我们先从数学和图像处理应用的意义上来看一下卷积到底是什么操作。我们先回到数学教科书中来看卷积，在泛函分析中，卷积也叫旋积或者褶积，是一种通过两个函数x(t)和h(t)生成的数学算子。其计算公式如下：

$$连续形式:\ \ \ \ x(t)*h(t) = \int_{-\infty}^{\infty}x(\tau)h(t-\tau)dt \\ 离散形式:\ \ \ \ x(t)*h(t) = \sum_{t=-\infty}^{\infty}x(\tau)h(t-\tau)$$

    从卷积公式可以看出，卷积就是先将一个函数进行翻转(Reverse)，然后再做一个平移(Shift)，这便是’卷’的含义。而’积’就是将平移后的两个函数对应元素相乘求和。所以卷积本质上就是一个Reverse-Shift-Weighted Summation的操作。

    我们使用图像来描述卷积的过程。

    多次乘积的和便是卷积的结果。

二、2D卷积

    我们从最原始的图像卷积操作开始。因为图像有单通道图像(灰度图)和多通道图(RGB图)，所以对应常规卷积方式可以分为单通道卷积和多通道卷积。二者本质上并无太大差异，无非对每个通道都要进行卷积而已。先来看单通道卷积。

    在单通道卷积中，针对图像的像素矩阵，卷积操作就是用一个卷积核来逐行逐列的扫描像素矩阵，并与像素矩阵做元素相乘，以此得到新的像素矩阵。其中卷积核也叫过滤器或者滤波器，滤波器在输入像素矩阵上扫过的面积称之为感受野。假设输入图像维度为$ nnc$，滤波器维度为$ ff1$，卷积步长为s，padding大小为p，那么输出维度可以计算为：

$$(\frac{n+2p-f}{s}+1)*(\frac{n+2p-f}{s}+1)$$

    单通道的卷积过程($ 以n=5,c=1,f=3,s=1,p=0为例$)如下：

    多通道卷积就是每一个通道的卷积核是不一样的，即卷积核的维度将会变为$ ffc$，之后将每一个通道卷积的结果相加。

    以$ n=5,c=3,f=3,s=1,p=0$为例，首先，卷积核的每一通道会与输入图像的每一个通道卷积，得到3个$ 33$ 的卷积结果，之后将这个3个$ 33$ 按相应位置相加，如下所示：

三、3D卷积

    将2D卷积增加一个深度维便可扩展为3D卷积。输入图像是3维的，滤波器也是3维的，对应的卷积输出同样是3维的。操作示意图如下:

    可以想象一下3D卷积的动态图。用一个$ 222$ 的3D滤波器对一个$ 444$ 的输入图像进行3D卷积，可以得到一个$ 333$ 的输出。

    我们可以把2D卷积的计算输出公式进行扩展，可以得到3D卷积的输出维度计算公式。假设输入图像大小为$ a_1a_2a_3$ ，通道数为c，过滤器大小为$ fff*c$ ，滤波器数量为n，则输出维度可以表示为：

$$(a_1-f)*(a_2-f)*(a_3-f)*n$$

    3D卷积在医学影像数据、视频分类等领域都有着较为广泛的应用。相较于2D卷积，3D卷积的一个特点就是卷积计算量巨大，对计算资源要求相对较高。

四、转置卷积

    转置卷积(Transposed Convolution)也叫解卷积(Deconvolution)，有些人也将其称为反卷积，但这个叫法并不太准确。大家都知道，在常规卷积时，我们每次得到的卷积特征图尺寸是越来越小的。但在图像分割等领域，我们是需要逐步恢复输入时的尺寸的。如果把常规卷积时的特征图不断变小叫做下采样，那么通过转置卷积来恢复分辨率的操作可以称作上采样。

    本质上来说，转置卷积跟常规卷积并无区别。不同之处在于先按照一定的比例进行padding来扩大输入尺寸，然后把常规卷积中的卷积核进行转置，再按常规卷积方法进行卷积就是转置卷积。假设输入图像矩阵为X，卷积核矩阵为C，常规卷积的输出为Y，则有：

$$Y=CX$$

    两边同时乘以卷积核的转置$ C^T$，这个公式便是转置卷积的输入输出计算。

$$X=C^TY$$

    注：这里$ C^T$ 并不代表矩阵C的转置，而是一个具有跟C的转置相同维度的一个矩阵，也可以称之为转置卷积的卷积核。

    假设输入大小为$ 44$ ，滤波器大小为$ 33$ ，常规卷积下输出$ 22$ ，为了演示转置卷积，我们将滤波器矩阵进行稀疏化处理为$ 416$ ，将输入矩阵进行拉平为$ 161$ ，相应输出结果也会拉平为41，图示如下：

    然后按照转置卷积的做法我们把卷积核矩阵进行转置，按照$ X=C^TY$进行验证：

    关于转置卷积的最后一个问题是输入输出尺寸计算。我们将常规卷积的计算公式转化一下即可得到转置卷积的换算公式：

$$w_1 = \frac{w_2+2p-f}{s}+1 \\ w_2 = s(w_1 - 1)+f-2p$$

    但当我们常规卷积出现$ (w_2+2p-f)\%s \ne0$ 时，我们转置卷积得到的图像就不会与原图像相匹配，因为，我们在卷积的时候舍去了一部分卷积结果，因此我们再反卷积的时候要把这部分加上来。如下图所示，在常规卷积时，最右侧与最下面一列舍去了，在此实验中padding=1,stride=2。

    于是我们修改了维度计算公式：

$$w_2 = s(w_1 - 1)+f-2p + (w_2+2p-f)\%s$$

    其对应的转置卷积过程如下(白色部分为填充内容，在最右侧与最下侧多添加了一行)：

五、1x1卷积

    1x1卷积的伟大发明来自于2014年GoogLeNet的inception v1，其主要作用在于可以降维节省计算成本。1x1卷积在卷积方式上与常规卷积并无差异，主要在于其应用场景和功能。

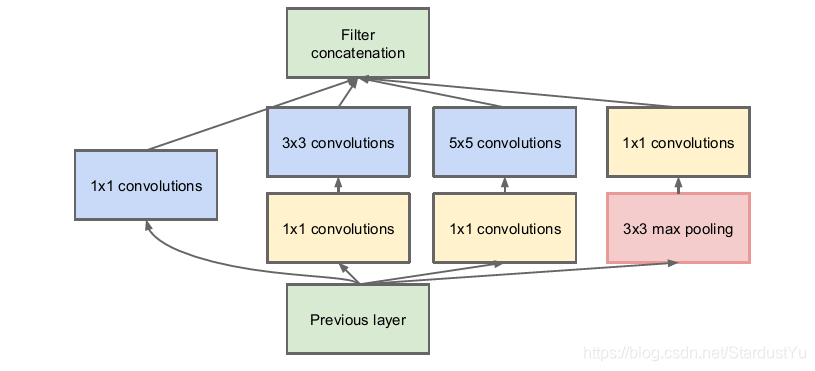
    下面我们来看1x1卷积到底有什么功效。假设现在我们有$ 2828192$ 的输入，使用32个$ 55192$ 的卷积核对其进行卷积，那么输出为$ 282832$ ，好像没什么特别之处。我们来看一下它的计算量，对于输出中的每一个元素值都要执行$ 55192$ 次计算，所以这次卷积的计算量为：$ 28283255192=120422400$ 。55卷积的运算量直接上亿了。

    那现在看看1x1卷积会如何。我们先用16个$ 11192$ 的卷积核对输入进行卷积，输出尺寸为$ 282816$ ，再用32个$ 5516$ 的卷积核对其进行卷积，输出为$ 282832$ 。经历两次卷积同样得到$ 282832$ 的输出，来看一下其中的计算量。第一次卷积：$ 282816192=2408448$ ，第二次卷积$ 2828325516=10035200$ ，两次卷积合计计算量约为120万，将较于直接的5*5卷积，1x1卷积的计算量直接减少了10倍，能够在保证网络性能的情况下极大幅度的节约计算成本。这便是1x1卷积。

六、深度可分离卷积

    从维度的角度看，卷积核可以看成是一个空间维(宽和高)和通道维的组合，而卷积操作则可以视为空间相关性和通道相关性的联合映射。从inception的1x1卷积来看，卷积中的空间相关性和通道相关性是可以解耦的，将它们分开进行映射，可能会达到更好的效果。

    深度可分离卷积是在1x1卷积基础上的一种创新。主要包括两个部分：深度卷积和1x1卷积。深度卷积的目的在于对输入的每一个通道都单独使用一个卷积核对其进行卷积，也就是通道分离后再组合。1x1卷积的目的则在于加强深度。下面以一个例子来看一下深度可分离卷积。

    假设我们用128个$ 333$ 的滤波器对一个$ 773$ 的输入进行卷积，可得到$ 55128$ 的输出,其计算量为$ 5512833*3=86400$ 。如下图所示：

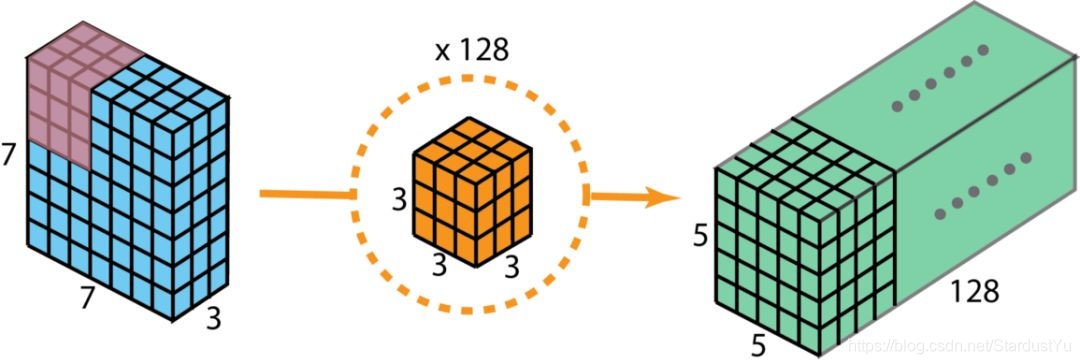
    现在看如何使用深度可分离卷积来实现同样的结果。深度可分离卷积的第一步是深度卷积。这里的深度卷积，就是分别用3个$ 331$ 的滤波器对输入的3个通道分别做卷积，也就是说要做3次卷积，每次卷积都有一个$ 551$ 的输出，组合在一起便是$ 553$ 的输出。

    现在为了拓展深度达到128，我们需要执行深度可分离卷积的第二步：1x1卷积。现在我们用128个$ 113$ 的滤波器对$ 553$ 进行卷积，就可以得到$ 55128$ 的输出。完整过程如下图所示：

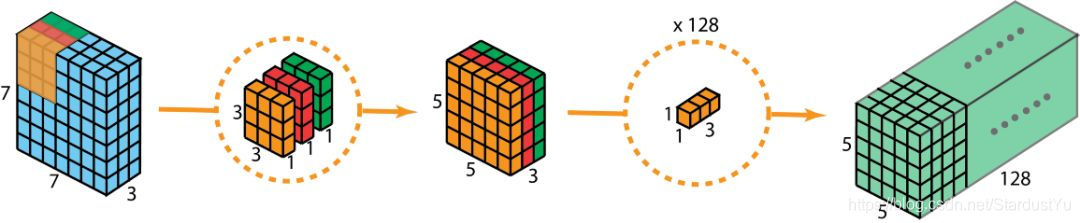
    那么我们来看一下深度可分离卷积的计算量如何。第一步深度卷积的计算量：$ 5513313=675$ 。第二步1x1卷积的计算量：$ 5512811*3=9600$ ，合计计算量为10275次。可见，相同的卷积计算输出，深度可分离卷积要比常规卷积节省12倍的计算成本。

    典型的应用深度可分离卷积的网络模型包括xception和mobilenet等。本质上而言，xception就是应用了深度可分离卷积的inception网络。

七、空洞卷积

    空洞卷积也叫扩张卷积或者膨胀卷积，简单来说就是在卷积核元素之间加入一些空格(零)来扩大卷积核的过程。我们用一个扩展率a来表示卷积核扩张的程度。比如说a=1,2,4的时候卷积核核感受野如下图所示，其中红点表示原卷积核的内容，其他颜色的为扩张的部分：

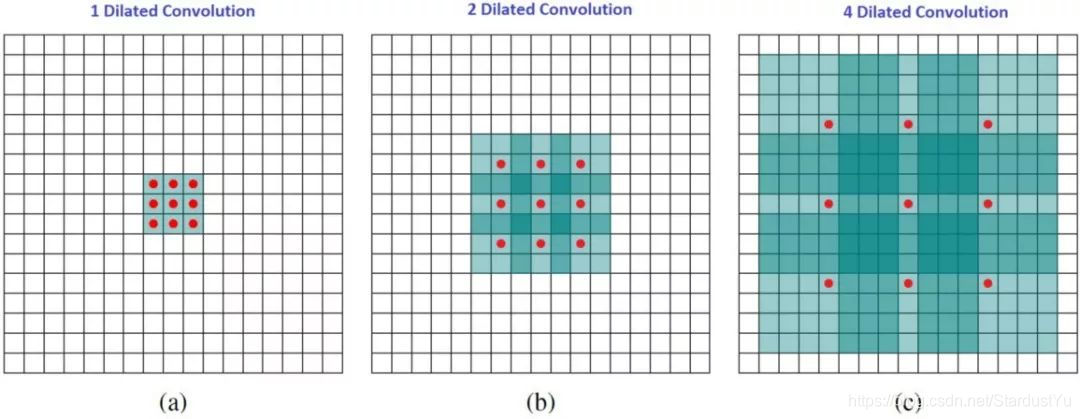
    加入空洞之后的实际卷积核尺寸与原始卷积核尺寸之间的关系：

$$K=k+(k-1)(a-1)$$

    其中k为原始卷积核大小，a为卷积扩展率，K为经过扩展后实际卷积核大小。除此之外，空洞卷积的卷积方式跟常规卷积一样。a=2时的空洞卷积的动态示意图如下所示：

    那么空洞卷积有什么好处呢？一个直接作用就是可以扩大卷积感受野，空洞卷积几乎可以在零成本的情况下就可以获取更大的感受野来扩充更多信息，这有助于在检测和分割任务中提高准确率。空洞卷积的另一个优点则是可以捕捉多尺度的上下文信息，当我们使用不同的扩展率来进行卷积核叠加时，获取的感受野就丰富多样。

八、图卷积

推荐博客通俗易懂：图卷积神经网络入门详解



`

`

参考链接：深度学习100问-6：有哪些经典的卷积类型？