AI小知识系列(一) 面试小知识(1)

AI小知识系列—第一节

1、神经网络反向传播公式推导

    神经网络的反向传播是借助计算图和链式法则来进行的

    以下面的函数为例，进行具体讲解：

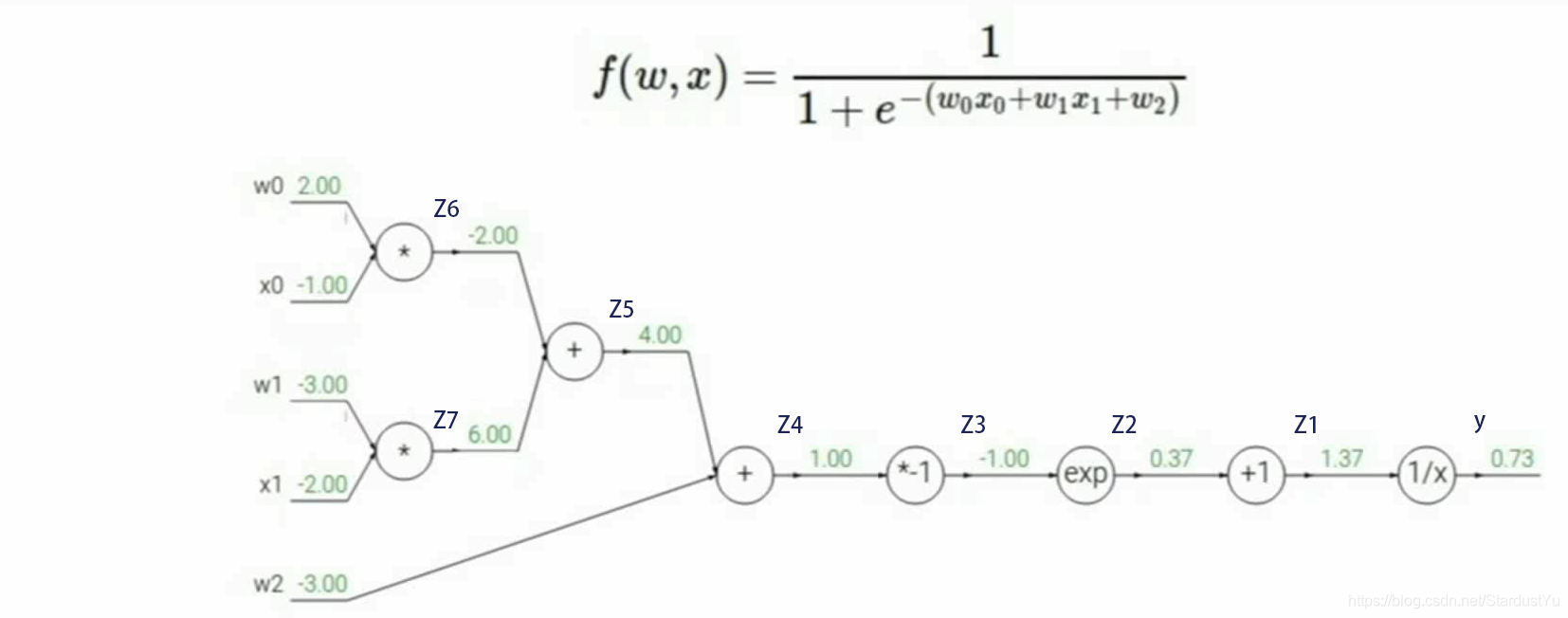
    首先，我们先要声明，在这里$ x_0,x_1$是这个函数的输入值，$ w_0，w_1$是这个函数的参数，也就是反向传播需要进行更新的参数。 Z1~Z8是中间值，y是计算得到的结果。

$$根据链式法则，依次计算梯度。\\ y = \frac{1}{Z_1} 且Z_1=1.37\Rightarrow \frac{\partial y}{\partial Z_1}=-\frac{1}{1.37^2} \\ Z_1 = 1+Z_2 \Rightarrow \frac{\partial Z_1}{\partial Z_2} = 1\Rightarrow \frac{\partial y}{\partial Z_2} = \Rightarrow \frac{\partial y}{\partial Z_1} ·\frac{\partial Z_1}{\partial Z_2} = -\frac{1}{1.37^2} \\ \Downarrow \\ ... \\ \Downarrow \\ \frac{\partial y}{\partial w_0} \ \ \frac{\partial y}{\partial w_1} \ \ \frac{\partial y}{\partial w_2} \\ \Downarrow \\ 更新w_0,w_1,w_2\\ w_0 =w_0 -\eta \frac{\partial y}{\partial w_0} \\ w_1 =w_1 -\eta \frac{\partial y}{\partial w_1} \\ w_2 =w_2 -\eta \frac{\partial y}{\partial w_2} \\ \eta 为学习率 \\ 到此反向传播完成。$$

2、Batch Normalization的反向传播过程

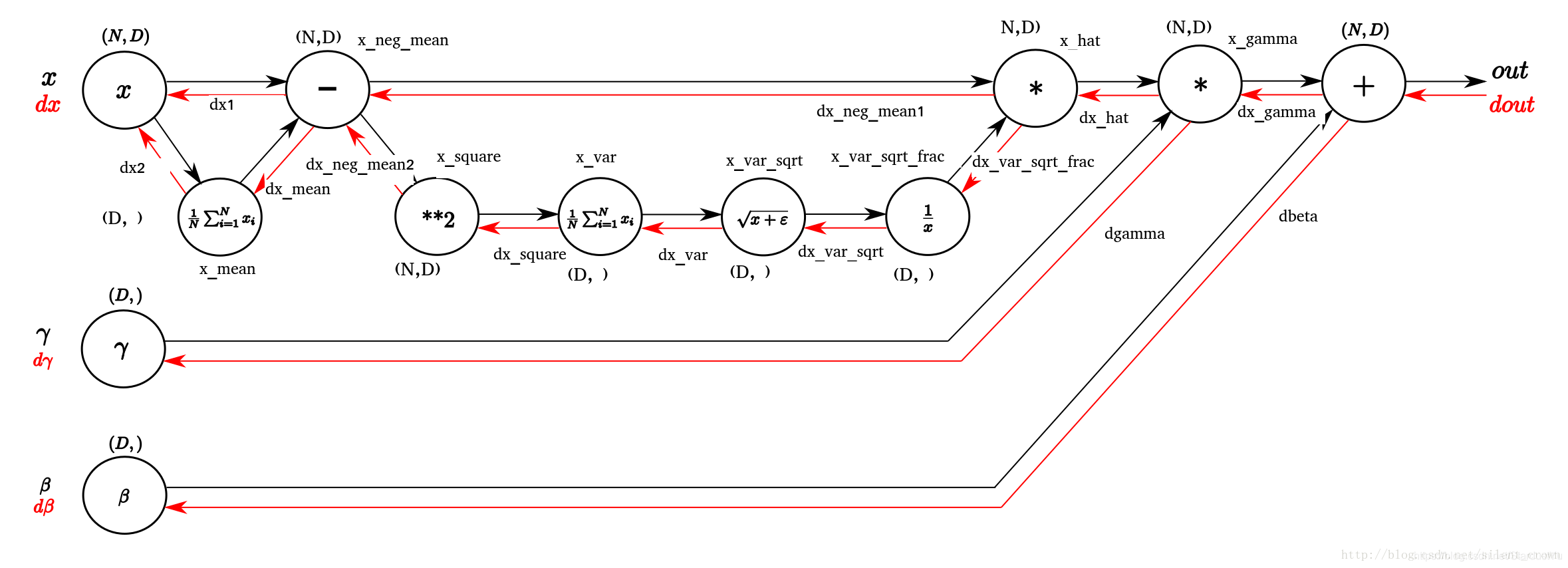
3、sigmoid的导数最大为0.25

    推导公式如下：

$$\sigma(x) = \frac{1}{1+e^{-x}} \\ \Downarrow \\ \sigma(x)' = \frac{e^{-x}}{(1+e^{-x})^2} \Rightarrow \sigma(x)' = \frac{e^{-x}}{1+(e^{-x})^2 + 2*e^{-x}} \Rightarrow \sigma(x)' = \frac{1}{\frac{1}{e^{-x}}+e^{-x} + 2}\le \frac{1}{4}$$

4、Softmax？Hardmax？

    这次要解决的是，Softmax为何叫Softmax，它Soft在何处？

    此处引用，https://zhuanlan.zhihu.com/p/34404607

    来看一下Softmax的表达式

$$p_i = \frac{e^{x_i}}{\sum_j e^{x_j}}$$

    与之相对应的表达式，我们可以称之为Hardmax

$$p_i = \frac{x_i}{\sum_j x_j}$$

    那么，Softmax与Hardmax的区别如下：

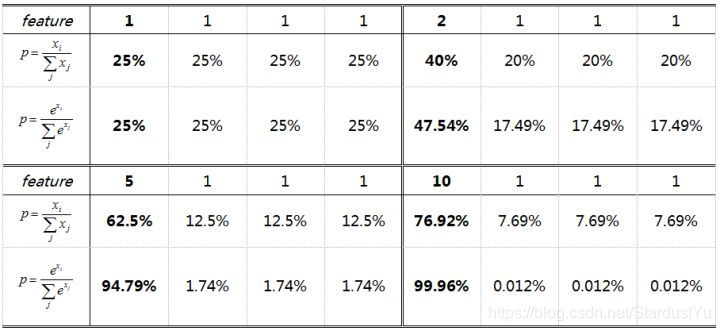
    Softmax是soft（软化）的max。在CNN的分类问题中，我们的ground truth是one-hot形式，下面以四分类为例，理想输出应该是（1，0，0，0），或者说（100%，0%，0%，0%），这就是我们想让CNN学到的终极目标。

    相同输出特征情况，Softmax比Hardmax更容易达到终极目标one-hot形式，或者说，softmax降低了训练难度，使得多分类问题更容易收敛。

    Softmax鼓励真实目标类别输出比其他类别要大，但并不要求大很多。Softmax鼓励不同类别的特征分开，但并不鼓励特征分离很多，如上表（5，1，1，1）时loss就已经很小了，此时CNN接近收敛梯度不再下降。

5、bagging vs boosting

    此处引用，https://blog.csdn.net/u013709270/article/details/72553282

    Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个性能更加强大的分类器。

    Bagging的算法过程如下：

1、 原始样本集中抽取训练集。每轮从原始样本集中使用自助法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

2、每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

3、对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

    Boosting的两个核心问题：

1、在每一轮如何改变训练数据的权值或概率分布？
    通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

2、通过什么方式来组合弱分类器？
    通过加法模型将弱分类器进行线性组合，比如AdaBoost通过加权多数表决的方式，即增大错误率小的分类器的权值，同时减小错误率较大的分类器的权值。

    两者的区别：

1）样本选择上：

    Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

    Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

    Bagging：使用均匀取样，每个样例的权重相等

    Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

    Bagging：所有预测函数的权重相等。

    Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

    Bagging：各个预测函数可以并行生成

    Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

最后：

1. Bagging + 决策树 = 随机森林
2. AdaBoost + 决策树 = 提升树
3. Gradient Boosting + 决策树 = GBDT

6、Batch-normalization与Layer-normalization

    Batch-normalization是在特征维度做normalization，是针对mini-batch所有数据的单个特征做的规范化。

    Layer-normalization是在样本维度做normalization，即对一个样本的所有特征做规范化。

    此处引入对三种normalization的好的解释的文章https://zhuanlan.zhihu.com/p/33173246

7、Normalization为什么会奏效

1. Normalization具有权重伸缩不变性（即对权重进行伸缩变换，规范化后的值是不变的），因此，这个性质就避免了反向传播因为权重过大或过小而造成的梯度问题，加速了收敛过程。同时这一属性也具有参数正则化的效果，避免了参数的大幅度震荡，提高了网络的泛化性能。
2. Normalization具有数据伸缩不变性，这一性质可以有效地减少梯度弥散，简化学习率的选择。
3. Normalization规范了每一层的数据输入，使得其分布一致，使得所有特征具有相同的均值和方差，这样这一层的神经元就不会因为上一层或下一层的神经元的剧烈变化而不稳定，也就加速了收敛。

8、鲁棒性vs泛化能力

    鲁棒性字面上理解可以认为是健壮性，健壮性可以认为是更好，更加抗风险的

    鲁棒性好代表该模型：

      1.模型具有较高的精度或有效性，这也是对于机器学习中所有学习模型的基本要求；
      2.对于模型假设出现的较小偏差，只能对算法性能产生较小的影响； 主要是：噪声（noise）
      3.对于模型假设出现的较大偏差，不可对算法性能产生“灾难性”的影响；主要是：离群点（outlier）

    在机器学习方法中，泛化能力通俗来讲就是指学习到的模型对未知数据的预测能力。在实际情况中，我们通常通过测试误差来评价学习方法的泛化能力。如果在不考虑数据量不足的情况下出现模型的泛化能力差，那么其原因基本为对损失函数的优化没有达到全局最优。

9、numpy实现卷积的优化操作im2col

    我们假设卷积核的尺寸为$ 2 2$ ，输入图像尺寸为$ 33$ 。im2col做的事情就是对于卷积核每一次要处理的小窗，将其展开到新矩阵的一行（列），新矩阵的列（行）数，就是对于一副输入图像，卷积运算的次数（卷积核滑动的次数），如下图所示：

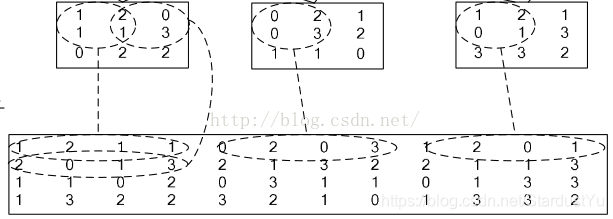
    以最右侧一列为例，卷积核为$ 2*2$ ，所以新矩阵的列数就为4；步长为一，卷积核共滑动4次，行数就为4.再放一张图应该看得更清楚。

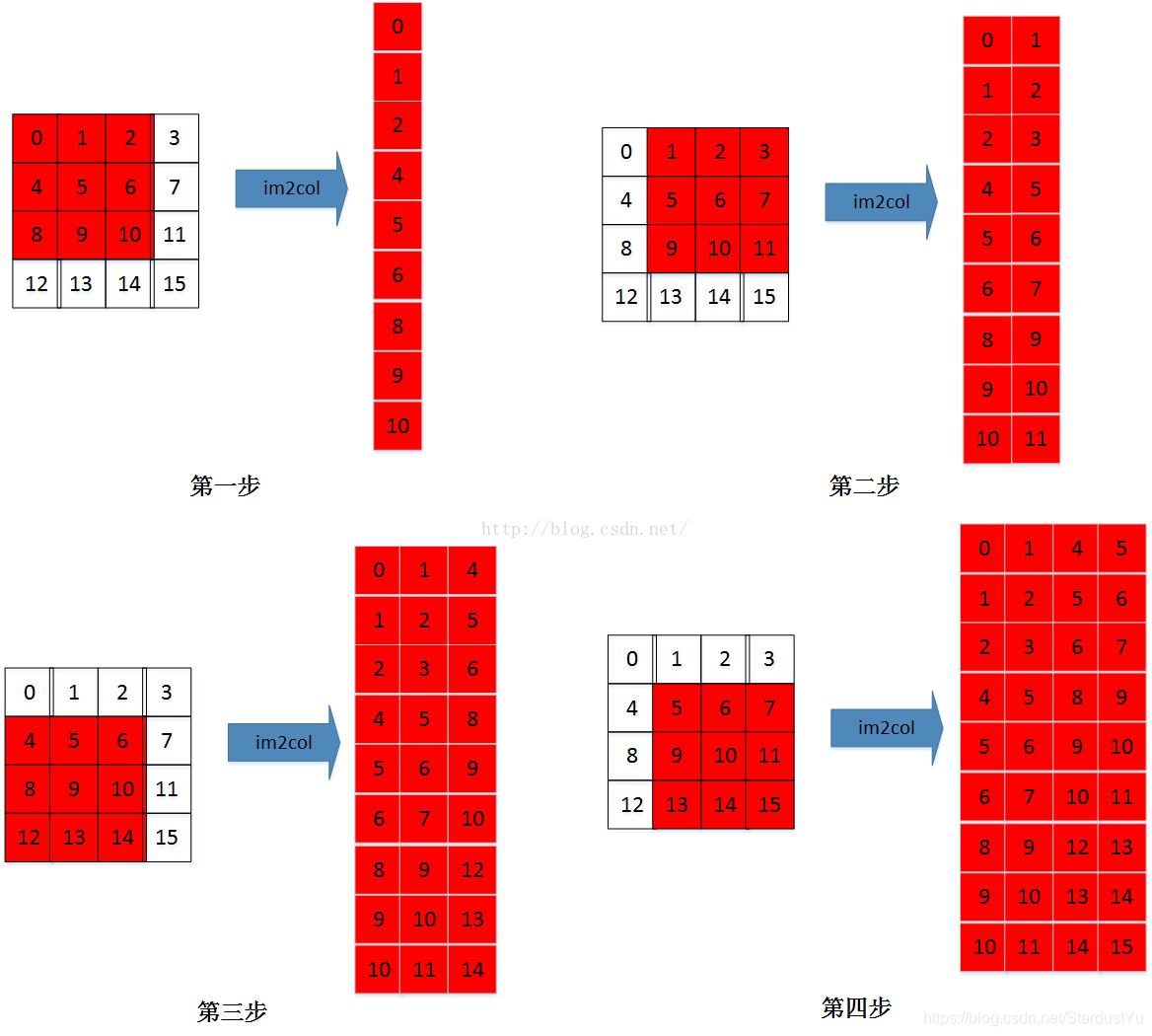
    输入为$ 44$ ，卷积核为$ 33$，则新矩阵为$ 9*4$ 。

    看到这里我就产生了一个疑问：我们把一个卷积核对应的值展开，到底应该展开为行还是列呢？卷积核的滑动先行后列还是相反？区别在哪？
    这其实主要取决于我们使用的框架访存的方式。计算机一次性读取相近的内存是最快的，尤其是当需要把数据送到GPU去计算的时候，这样可以节省访存的时间，以达到加速的目的。不同框架的访存机制不一样，所以会有行列相反这样的区别。在caffe框架下，im2col是将一个小窗的值展开为一行，而在matlab中则展开为列。所以说，行列的问题没有本质区别，目的都是为了在计算时读取连续的内存。
    这也解释了我们为什么要通过这个变化来优化卷积。如果按照数学上的步骤做卷积读取内存是不连续的，这样就会增加时间成本。同时我们注意到做卷积对应元素相乘再相加的做法跟向量内积很相似，所以通过im2col将矩阵卷积转化为矩阵乘法来实现。
im2col的代码如下：

def im2col(image, ksize, stride):
    # image is a 4d tensor([batchsize, width ,height, channel])
    image_col = []
    for i in range(0, image.shape[1] - ksize + 1, stride):
        for j in range(0, image.shape[2] - ksize + 1, stride):
            col = image[:, i:i + ksize, j:j + ksize, :].reshape([-1])
            image_col.append(col)
    image_col = np.array(image_col)
    return image_col

此处引用文章https://blog.csdn.net/dwyane12138/article/details/78449898