1、模型介绍

支持向量机 SVM 模型，它利用了软间隔最大化、拉格朗日对偶、凸优化、核函数、序列最小优化等方法。支持向量机既可以解决线性可分的分类问题，也可完美解决线性不可分问题。

支持向量是距离分类超平面近的那些点，SVM 的思想就是使得支持向量到分类超平面的间隔最大化。

1.1 模型

对于模型输入$ x$ ，模型参数$ w$ ，模型输出$ h(x) $ ，预测结果$ y\in{0,1}$

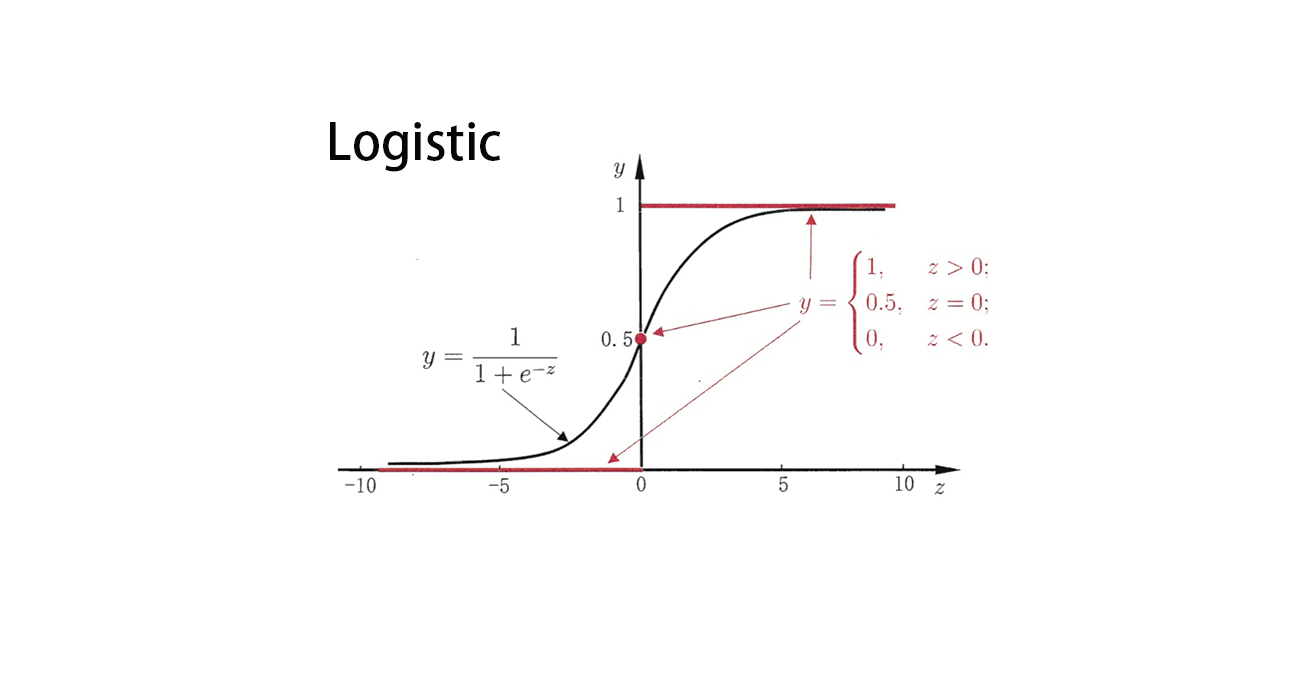
$h(x) = g(w^Tx) = \frac{1}{1+e^{-w^Tx}} \\ y = \begin{cases} 0 & & if&h(x)<C\\ 1 & & if&h(x)>C \end{cases}$

其中$ g(x)$ 是Sigmoid函数，其函数形式如下：

$g(x) = \frac{1}{1+e^{-x}}$

其中$ C$ 是一个常数，是分类阈值，通常取0.5

1.2 SVM原理介绍

SVM也是一种线性的分类器，我们需要得到其权重$ w$，首先，要找到其目标函数与约束条件

1.2.1 软间隔最大化

我们假设，SVM的分类超平面为$ w^Tx+b=0$ ，点到平面的距离为$ d = \frac{|w^Tx+b|}{||w||}$，输入样本$ x_i$ ，对应的label为$ y_i \in {-1,1}$。

我们可以得到，样本$ x_i$到分类超平面的距离

$r_i = y_i(\frac{w^Tx+b}{||w||})$

根据SVM的原理，我们需要找到距离超平面最近的点，即支持向量：

$r = min \ r_i$

同时，我们知道，支持向量离超平面越远越好，这就我们就得到了其目标函数和约束条件：

$max \ r \\ s.t \quad r_i=y_i(\frac{w^Tx+b}{||w||}) \ge r$

稍加转变，令$ r=\hat{r} /||w||$，则上面的目标函数变成：

$max \ \frac{\hat{r}}{||w||} \\ s.t \quad y_i(w^Tx_i+b) \ge \hat{r}$

由于 w, b 成倍数变化并不会影响超平面的公式，我们不妨让$ w’ = w/\hat{r}，b’ = w/\hat{b}$ ，变换完成后，再令$ w = w’,b = b’$ 。得到目标函数与约束条件。

$max \ \frac{1}{||w||} \\ s.t \quad y_i(w^Tx_i+b) \ge 1$

上面的目标函数和约束条件，对于所有的点必须严格成立才行。而总会有数据，是一个超平面分不开的，会有一些特异点：

为了解决这个问题，我们要引入松弛变量，使其约束条件变成：

$s.t. \quad y_i(w^Tx_i+b) + \epsilon_i \ge 1 \\ \epsilon_i \ge 0$

同时，我们可以将目标函数进行更改，修改为：

$max\ \frac{1}{||w||} \Rightarrow min\ \frac{1}{2}||w||^2$

所以，我们最后得到的目标函数与约束条件为：

$min\ \frac{1}{2}||w||^2+C\sum \epsilon_i \\ s.t. \quad y_i(w^Tx_i+b) + \epsilon_i \ge 1 \\ \epsilon_i \ge 0$

其中，C为惩罚参数，它的目的是使得目标变量最小即几何间隔最大，且使得松弛变量最小化。加入松弛变量的目标函数就是软间隔最大化。

1.2.2 拉格朗日对偶

我们需要使用拉格朗日乘子法来对上面的凸二次优化问题进行求解，得到的拉格朗日函数如下：

$L(w,b,\epsilon,\alpha,\mu) =\frac{1}{2}||w||^2+C\sum \epsilon_i - \sum \alpha_i(y_i(w^Tx_i+b)-1+\epsilon_i) - \sum \mu_i \epsilon_i \\ \alpha_i \ge 0,\mu_i \ge 0$

从上式可以看出，$ \alpha=0,\mu = 0$ 可使上式最大，即：

$max_{\alpha,\mu}L(w,b,\epsilon,\alpha,\mu) =\frac{1}{2}||w||^2+C\sum \epsilon_i$

因此，原目标函数就变成了：

$min_{w,b,\epsilon} max_{\alpha,\mu} L(w,b,\epsilon,\alpha,\mu)$

而求解上面的问题很困难，我们要对其进行转换，利用拉格朗日对偶性，可通过求解原最优化问题的对偶问题得到原问题的最优解。原最优化问题的对偶问题为：

$max_{\alpha,\mu} min_{w,b,\epsilon} L(w,b,\epsilon,\alpha,\mu)$

利用拉格朗日的对偶性，将问题转换成了极大极小化拉格朗日函数的问题

1.2.3 最优化问题求解

对于极大极小化拉格朗日函数的问题，首先要求解关于拉格朗日函数的极小化问题。

对三个变量分别求偏导得：

$\frac{\partial L}{\partial w} = w - \sum \alpha_iy_ix_i=0 \\ \frac{\partial L}{\partial b} = - \sum \alpha_iy_i=0 \\ \frac{\partial L}{\partial \epsilon_i} = C - \alpha_i - \mu_i =0$

将以上三式带入拉格朗日函数中得：

$min_{w,b,\epsilon} L = -\frac{1}{2}\sum\sum\alpha_i\alpha_jy_iy_j(x_i·x_j) + \sum \alpha_i$

那么极大极小化拉格朗日函数转换成：

$max_{\alpha,\mu} min_{w,b,\epsilon} L = min_{\alpha,\mu} \frac{1}{2}\sum\sum\alpha_i\alpha_jy_iy_j(x_i·x_j) - \sum \alpha_i \\ s.t. \quad \sum \alpha_iy_i=0 \\ \quad \quad \quad 0 \le \alpha_i \le C$

1.2.4 核函数

对于线性不可分问题，这类问题是无法用超平面划分正负样本数据的，但如果我们可以把原本不可分的数据转换成线性可分的数据，那么我们就可以用SVM进行求解。如下图所示：

对于左侧的情况，我们使用了一个曲面作为分类边界，而当我们转换成右侧的坐标系中后，我们就可以使用SVM进行解决了。

对于曲面分类边界，其函数形式为：

$k_1x_1^2 + k_2x_2^2 + k_3x_1 + k_4x_2 + k_5x_1x_2 + k_6 = 0$

映射到新坐标系中：

$z_1 = x_1^2,z_2 = x_2^2,z_3 = \sqrt{2}x_1,z_4 = \sqrt{2}x_2,z_5 = \sqrt{2}x_1x_2$

那么在新的坐标系下，其超平面为：

$k_1'z_1 + k_2'z_2 + k_3'z_3 + k_4'z_4 + k_5'z_5 + k_6'=0$

也就是将在二维空间(x1,x2)下线性不可分的问题转换成了在五维空间(z1,z2,z3,z4,z5)下线性可分的问题。

那么，在二维空间中，对于两个点$ p,q$ 的内积，我们有$ (p·q) = (p_1·q_1+p_2·q_2)$ ,当将其转换到五维空间后，他们的内积，则为$ (\varphi(p),\varphi(q)) = p_1^2q_1^2+p_2^2q_2^2+2p_1q_1+2p_2q_2+2p_1q_1p_2q_2$ 。

那么我们可以定义一个核函数$ k(p,q)$，使得：

$k(p,q) = ((p·q)+1)^2 = p_1^2q_1^2+p_2^2q_2^2+2p_1q_1+2p_2q_2+2p_1q_1p_2q_2 = (\varphi(p),\varphi(q)) + 1$

所以，我们使用核函数，可以根据低维空间的数据，得到高维空间的内积，利用核函数，无需先将变量一一映射到高维空间再计算内积，而是简单得在低维空间中利用核函数完成这一操作。

那么，我们为什么要用内积呢，因为在上面的优化函数里，我们只需要计算两个点的内积即可。因此，原目标函数变为：

$max_{\alpha} min_{w,b,\epsilon} L = min_{\alpha,\mu} \frac{1}{2}\sum\sum\alpha_i\alpha_jy_iy_jK(x_i·x_j) - \sum \alpha_i \\ s.t. \quad \sum \alpha_iy_i=0 \\ \quad \quad \quad 0 \le \alpha_i \le C$

1.2.5 序列最小优化 (Sequential minimal optimization)

到目前为止，优化问题已经转化成了一个包含 N 个 $ \alpha$ 自变量的目标变量和两个约束条件。由于目标变量中自变量 $ \alpha$ 有 N 个，为了便与求解，每次选出一对自变量 $ \alpha$ ，然后求目标函数关于其中一个 $ \alpha$ 的偏导，这样就可以得到这一对 $ \alpha$ 的新值。给这一对 $ \alpha$ 赋上新值，然后不断重复选出下一对 $ \alpha$ 并执行上述操作，直到达到最大迭代数或没有任何自变量 $ \alpha$ 再发生变化为止，这就是 SMO 的基本思想。说直白些，SMO 就是在约束条件下对目标函数的优化求解算法。

为何不能每次只选一个自变量进行优化？那是因为只选一个自变量 $ \alpha$ 的话，会违反第一个约束条件，即所有$ \alpha$ 和 y 值乘积的和等于 0。

选择两个自变量

下面是详细的 SMO 过程。假设选出了两个自变量分别是$ \alpha_1$ 和$ \alpha_2$ ，除了这两个自变量之外的其他自变量保持固定，则目标变量和约束条件转化为：

$min_{\alpha_1,\alpha_2}L(\alpha_1,\alpha_2) = \frac{1}{2}K_{11}\alpha_1^2 + \frac{1}{2}K_{22}\alpha_2^2 + y_1y_2K_{12}\alpha_1\alpha_2- \\(\alpha_1+\alpha_2)+y_1\alpha_1\sum_{i=3}^Ny_i\alpha_iK_{i1}+y_2\alpha_2\sum_{i=3}^Ny_i\alpha_iK_{i2} \\ s.t. \quad \alpha_1y_1+\alpha_2y_2 = -\sum_{i=3}^Ny_i\alpha_i = \delta \\ \quad 0 \le \alpha_i \le C$

求 $ \alpha_2^{new,unc}$

将约束条件中的 $ \alpha_1$ 用 $ \alpha_2$ 表示，并代入目标函数中，则将目标函数转化成只包含 $ \alpha_2$ 的目标函数，让该目标函数对 $ \alpha_2$ 的偏导等于 0，可求得 $ \alpha_2$ 未经修剪的值：

$\alpha_2^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1 - E_2)}{\epsilon} \\ \epsilon = K_{11}+K_{22}-2K_{12} \\ E_i = f(x_i) - y_i = \sum_{j=1}^N\alpha_j y_j K(x_j,x_i)+b - y_i$

修剪 $ \alpha_2$

之所以说$ \alpha_2$ 是未经修剪的值是因为所有 alpha 都必须满足大于等于 0 且小于等于 C 的约束条件，用此约束条件将 $ \alpha_2$ 进行修剪，修剪过程如下：

$\alpha_1^{old}y_1+\alpha_2^{old}y_2 = \alpha_1^{new}y_1 + \alpha_2^{new}y_2 \\ 0 \le \alpha_1^{new} \le C \\ 0 \le \alpha_2^{new} \le C$

由此可得：

$0 \le \frac{\alpha_1^{old}y_1+\alpha_2^{old}y_2 - \alpha_2^{new}y_2}{y_1} \le C \\ 0 \le \alpha_2^{new} \le C$

分两种情况讨论：

情况 1.当 y1 等于 y2 时，有：

$\alpha_1^{old}+\alpha_2^{old}-C \le \alpha_2^{new} \le \alpha_1^{old} + \alpha_2^{old} \\ 0 \le \alpha_2^{new} \le C \\ L = max(0,\alpha_1^{old}+\alpha_2^{old}-C) \\ H = min(C,\alpha_1^{old}+\alpha_2^{old})$

情况 2.当 y1 不等于 y2 时，有：

$\alpha_2^{old}-\alpha_2^{old} \le \alpha_2^{new} \le C - \alpha_1^{old} + \alpha_2^{old} \\ 0 \le \alpha_2^{new} \le C \\ L = max(0,\alpha_2^{old}-\alpha_2^{old}) \\ H = min(C,C - \alpha_1^{old} + \alpha_2^{old} )$

修剪后，可得 alpha2 的取值如下：

$\alpha_2^{new} = \begin{cases} H & & \alpha_2^{new,unc} \ge H\\ \alpha_2^{new,unc} & & L \le \alpha_2^{new,unc} \le H \\ L & & \alpha_2^{new,unc} \le L \end{cases}$

得到$ \alpha_1$

由 $ \alpha_2$ 和 $ \alpha_1$ 的关系，可得：

$\alpha_1^{new} = \alpha_1^{old} + y_1y_2(\alpha_2^{old} - \alpha_2^{new})$

更新阈值b

当我们更新了一对$ \alpha_1,\alpha_2$之后都需要重新计算阈值 $ b$ ，因为 $ b$关系到我们$ f(x)$ 的计算，关系到下次优化的时候误差$ E_i$ 的计算。在完成 $ \alpha_1$ 和 $ \alpha_2$ 的一轮更新后，我们来更新 b 的值，

由$ y = w^Tx+b$ 以及KKT条件$ w=\sum \alpha_i y_i x_i$ 可知:

当 $ \alpha_1$ 更新后的值满足 $ 0 \le \alpha_1 \le C$ 时：

$\sum \alpha_iy_iK(x_i,x_1) + b = y_1$

根据上式，我们可以得出：

$b_1 = -E_1 -y_1K_{11}(\alpha_1^{new} - \alpha_1^{old}) - y_2K_{21}(\alpha_2^{new} - \alpha_2^{old}) + b^{old}$

同样的，当 $ \alpha_2$ 更新后的值满足 $ 0 \le \alpha_2 \le C$ 时：

$b_2 = -E_2 -y_1K_{12}(\alpha_1^{new} - \alpha_1^{old}) - y_2K_{22}(\alpha_2^{new} - \alpha_2^{old}) + b^{old}$

若更新后的 $ \alpha_1$ 和 $ \alpha_2$ 同时满足大于 0 且小于 C 的条件，那么 b = b1=b2;否则，b =(b1+b2)/2。

如何选择 $ \alpha_1$ 和 $ \alpha_2$

在程序开始时，初始化所有的$ \alpha$ 为0（当$ \alpha$ 已知时，所有的参数都能够计算得到）

$ \alpha_1$ 的选择

SMO称选择第1个变量的过程为外层循环。在这里我们在整个样本集和非边界样本集间进行交替。

首先，我们对整个训练集进行遍历，要选择一个违背下面的KKT条件的$ \alpha$ 为$ \alpha_1$ ：

$y_i f(x_i) \begin{cases} \ge 1 & & \alpha=0(样本点落在最大间隔外(分类完全正确的那些样本))\\ = 1 & & L \le \alpha \le H(样本点刚好落在最大间隔边界上) \\ \le 1 & & \alpha=C (样本点落在最大间隔内部) \end{cases}$

在遍历了整个训练集并优化了相应的$ \alpha$ 后第二轮迭代我们仅仅需要遍历其中的非边界$ \alpha$ . 所谓的非边界$ \alpha$ 就是指那些不等于边界0或者C的$ \alpha$ 值。因为这些样本点更容易违反KKT条件

之后就是不断地在两个数据集中来回交替，最终所有的$ \alpha$ 都满足KKT条件的时候，算法中止。

$ \alpha_2$ 的选择

SMO称选择第2个变量为内层循环。

当我们已经选取第一个 $ \alpha_1$ 之后，我们希望我们选取的第二个变量 $ \alpha_2$ 优化后能有较大的变化。根据我们之前推导的式子$ \alpha_2^{new,unc} = \alpha_2^{old} + \frac{y_2(E_1 - E_2)}{\epsilon}$ 可以知道，新的 $ \alpha_2$ 的变化依赖于|E1−E2|, 当E1为正时，那么选择最小的Ei作为E2，通常将每个样本的Ei缓存到一个列表中，通过在列表中选择具有|E1−E2|的α2来近似最大化步长。