1、模型介绍
不同于PCA方差最大化理论,LDA算法的思想是将数据投影到低维空间之后,使得同一类数据尽可能的紧凑,不同类的数据尽可能分散。LDA也是一种线性分类器,其不需要迭代式的进行训练,可以根据数据集,利用优化算法直接得到权重。LDA是一种多分类的线性分类器,是一种监督学习模型。
LDA有如下两个假设:
(1) 原始数据根据样本均值进行分类。
(2) 不同类的数据拥有相同的协方差矩阵。

1.1 模型
对于N分类问题,模型输入$ x$ ,模型参数$ w$ ,模型输出$ h(x)$ (N维向量),预测标签$ y$
1.2 权重计算过程
我们先以二分类任务为例,进行数学公式的推导。$ D$ 表示数据集,$ D_i$ 表示类别$ i$ 的数据。
计算类别 i 数据的原始中心点:
计算类别 i 数据投影后的中心点:
其用来衡量投影后,不同类别间的距离
得到每个数据投影后的点:
计算类别 i 数据投影后的方差(数据之间的分散程度)
其用来衡量投影后,同一类别内数据的距离
最终,得到投影后的损失函数(二分类)
对上面的式子进行带入展开
我们记$ S_B=(\mu_1 - \mu_2)(\mu_1 - \mu_2)^T$ ,$ S_i = \sum_{x\in D_i}(x-\mu_i)(x-\mu_i)^2$ ,$ S_w = \sum_i^NS_i$
则上面的式子,我们可以简化为:
推广到多分类
在多分类任务中,$ S_B$ 等于所有的$ \mu$ 两两相减的平方 的加和,$ S_w$ 等于所有的$ S_i$ 的加和
使用拉格朗日乘子法求解权重
在拉格朗日乘子法中,我们需要对分母进行限制,限制其等于1。这个限制条件跟SVM中的限制是一个道理,是为了防止权重的倍数增长而造成的有无穷多个解的问题,比如1/1=1,而2/2=1,我们加了限制条件,就只有了第一种可能性,这让我们可以使用拉格朗日算法
我们可以利用线性代数求特征值的方法求解w
2、模型分析
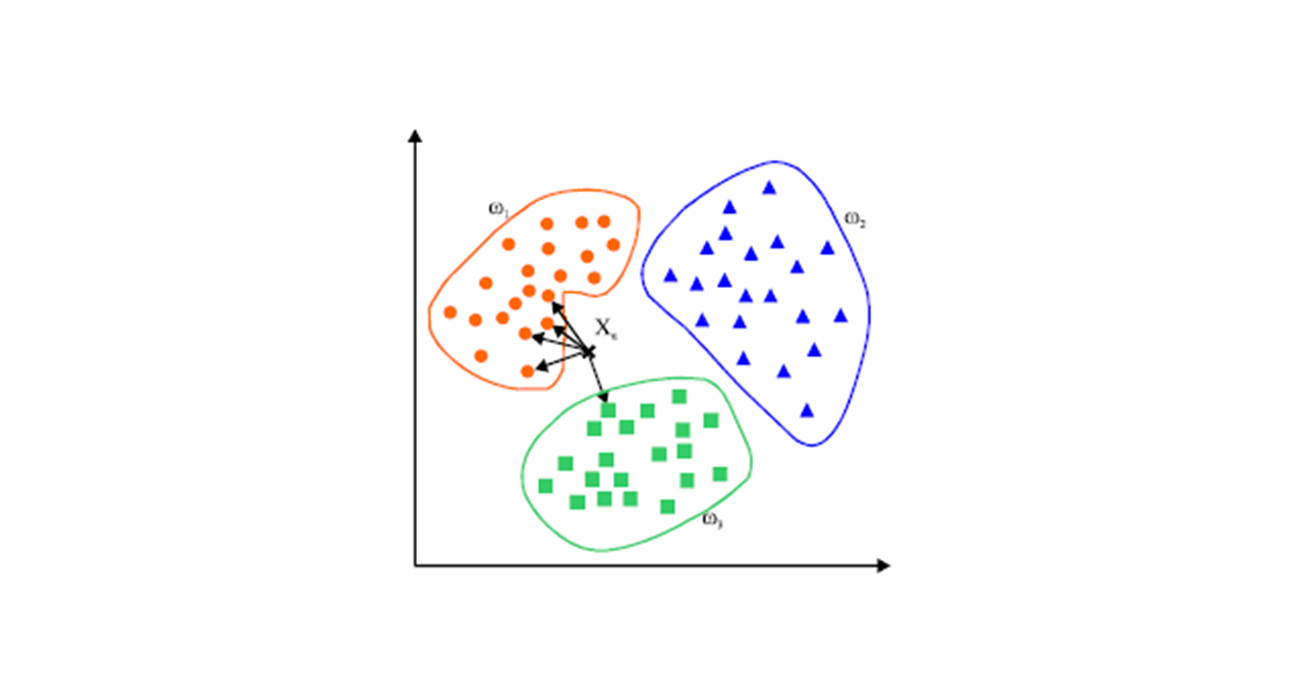
2.1 LDA与PCA
LDA是一种利用降维方法而得出的线性分类器,PCA是一种降维方法。我们可以根据降维这个话题,来分析这两个模型。LDA在降维时,主要利用了模型的均值,来进行类别的区分,而PCA则是使用了方差。如图:

2.2 模型优缺点
优点
- 计算速度快
- 充分利用了先验知识
缺点
- 当数据不是高斯分布时候,效果不好,PCA也是。
- 降维之后的维数最多为 类别数-1,因为在进行拉格朗日求解时,我们能够得到的特征向量的数目为x的秩-1。
2.3 模型应用
- 可以用于多分类任务中
- 降维之后的维数最多为类别数-1。所以当数据维度很高,但是类别数少的时候,算法并不适用。
参考链接