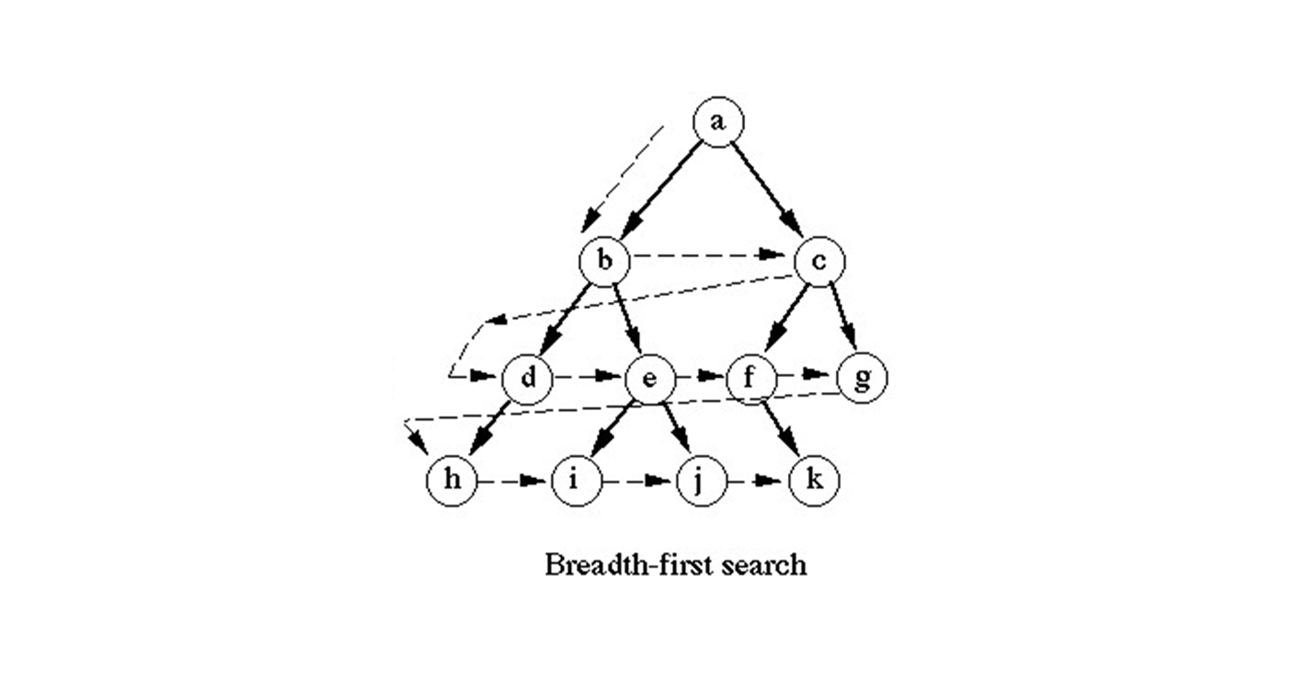
深度优先搜索 深度优先搜索(缩写DFS)有点类似广度优先搜索,也是对一个连通图 进行遍历 的算法。它的思想是从一个顶点V0开始,沿着一条路一直走到底,如果发现不能到达目标解,那就返回到上一个节点,然后从另一条路开始走到底,这种尽量往深处走的概念即是深度优先的概念。
深度优先搜索需要一个栈 ,将经过的节点push进栈中,等返回时,再pop出来
1、基本流程 1)DFS遍历过程 遍历整个图
2、算法比较与应用 BFS VS DFS
BFS是用来搜索最短径路的解 是比较合适的,比如求最少步数的解,最少交换次数的解,因为BFS搜索过程中遇到的解一定是离根最近的,所以遇到一个解,一定就是最优解,此时搜索算法可以终止。而DFS搜索到的解不一定是离根最近的,只有全局搜索完毕,才能从所有解中找出离根的最近的解。
空间代价 上,DFS是有优势的,DFS不需要保存搜索过程中的状态,而BFS在搜索过程中需要保存搜索过的状态,而且一般情况需要一个队列来记录。DFS适合搜索全部的解,因为要搜索全部的解,那么BFS搜索过程中,遇到离根最近的解,并没有什么用,也必须遍历完整棵搜索树,DFS搜索也会搜索全部,但是相比DFS不用记录过多信息,所以搜素全部解的问题,DFS显然更加合适。
3、经典题目 1)根节点出发的最大路径和问题 问题
给定一个非空 二叉树,返回其从根节点出发的最大路径和。
举例
1 2 3 4 5 6 7 8 9 输入: [-10,9,20,None,None,15,7] -10 / \ 9 20 / \ 15 7 输出: 25
思路
我们对路径进行遍历,找出其从各个节点出发的最大路径和
树的构建
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class TreeNode : def __init__ (self, x) : self.val = x self.left = None self.right = None def initTree (tree,i) : if tree[i] is None : return None if i < len(tree): root = TreeNode(tree[i]) if i*2 +1 < len(tree): root.left = initTree(tree,i*2 +1 ) if i*2 +2 < len(tree): root.right = initTree(tree,i*2 +2 ) return root tree = [-10 ,9 ,20 ,None ,None ,15 ,7 ] root = initTree(tree,0 )
递归遍历
1 2 3 4 5 6 def DFS (root:TreeNode) ->int: if root is None : return 0 left = max(DFS(root.left),0 ) right = max(DFS(root.right),0 ) return root.val+ max(left,right)
栈实现DFS
使用栈无法得到路径和,因此在这部分,我们计算树的总和,同时使用了List的数据结构作为树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def DFS (tree:List[int]) ->int: s = tree[0 ] Q = [] label = [False ]*len(tree) Q.append(0 ) label[0 ] = True while (len(Q) != 0 ): index = Q[-1 ] left = 2 *index+1 right = 2 *index+2 if (left < len(tree) and not label[left] and tree[right]): label[left] = True Q.append(left) s += tree[left] continue if (right < len(tree) and not label[right] and tree[right]): label[right] = True Q.append(right) s += tree[right] continue Q.pop(-1 ) return s
2)整个树的最大路径问题 leetcode—题124二叉树中的最大路径和
问题
给定一个非空 二叉树,返回其最大路径和
示例
1 2 3 4 5 6 7 8 9 输入: [-10,9,20,null,null,15,7] -10 / \ 9 20 / \ 15 7 输出: 42 (15--20--7这个路径和最大)
思路
我们根据第一题可以知道,我们可以用DFS计算某一条路径的和,那么我们可以使用DFS得到包括根节点的路径和node.val + max(left,right) ,同时,我们也可以计算以某一结点(非根节点)为开头的路径和,比如这里的15--20--7,我们完全可以通过node.val + left + right得到,因此,我们在递归使用DFS时,得到包括根节点的路径和,再从内部逻辑得到最大路径
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def DFS (root:TreeNode) ->int: def max_gain (node) : nonlocal max_sum if node is None : return 0 left = max(max_gain(node.left),0 ) right = max(max_gain(node.right),0 ) node_gain = node.val + left + right max_sum = max(max_sum,node_gain) return node.val + max(left,right) max_sum = -math.inf max_gain(root) return max_sum
3)矩阵中的路径问题 leetcode—剑指offer面试题12 矩阵中的路径
问题
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。
示例
例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[[“a”,”b “,”c”,”e”],f “,”c “,”s”],e “,”e”]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
思路
遍历矩阵中的每一个结点,将其作为DFS的开始节点,进行DFS的搜索过程,要注意的是,DFS经过的字符在之后的搜索中不能再进入,因此在DFS经过该字符时,我们要对该字符进行替换处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def exist (board: List[List[str]], word: str) -> bool: def dfs (i,j,k) : if i<0 or i>=len(board) or j < 0 or j>=len(board[0 ]) or board[i][j] != word[k]: return False if k == len(word)-1 : return True tmp,board[i][j] = board[i][j] , "/" res = (dfs(i,j-1 ,k+1 ) or dfs(i,j+1 ,k+1 ) or dfs(i-1 ,j,k+1 ) or dfs(i+1 ,j,k+1 )) board[i][j] = tmp return res for i in range(len(board)): for j in range(len(board[0 ])): if dfs(i,j,0 ): return True return False
参考链接