Long Short Term Memory networks
介绍:本篇介绍NLP中的特征提取器,LSTM以及其变种GRU
1、LSTM简介

上一节讲到,RNN存在一个很严重的问题,即,无法联系长期的依赖关系,也就是说,在经过多次的循环后,该时刻往往得不到很久之前的特征信息,同时,RNN很容易就梯度消失和梯度爆炸,而,LSTM的存在就是为了解决这两个问题。
我们都知道,原始的RNN中是利用隐藏层的输出$ h$ 来建立前后的依赖关系的,但是$ h$ 对于短期输入非常敏感,因此很容易受到短期输入的巨大影响导致丢失长期的影响。那么,我们在原来的基础上再添加一个状态$ C$ ,单独让$ C$ 来存储长期的状态,那就解决了这个问题,LSTM就是这样做的。而$ C$ 也被称为单元状态。
那么,LSTM是如何计算$ C$ ,即怎样维持长期的依赖关系呢?LSTM利用门结构来处理长期依赖与短期信息的关系,门结构可以实现选择性的让信息通过,其实际上就是一层全连接层,他的输入是一个向量,输出是一个0到1之间的使出向量,即$ g(x) = \sigma(Wx+b)$ 。在LSTM中主要有三个门结构,遗忘门、输入门和输出门。
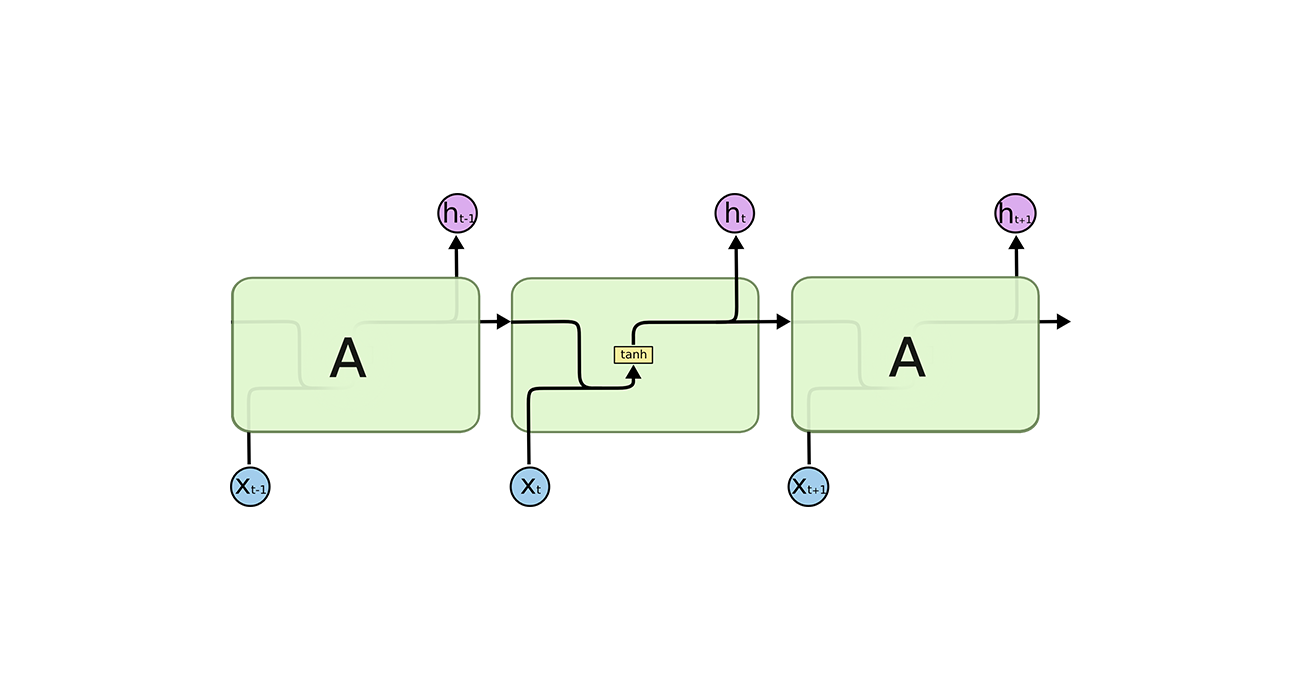
LSTM的主要结构如上图所示。可以看到,在$ t$ 时刻,LSTM的输入有三个,当前时刻的输入值$ x_{t-1}$ ,上一时刻的输出值$ h_{t-1}$ ,以及上一时刻的单元状态$ c_{t-1}$ 。LSTM的输出有两个,当前时刻的输出值$ h_t$ ,当前时刻的单元状态$ c_t$ 。
2、门结构
LSTM利用门结构来处理长期依赖与短期信息的关系,门结构可以实现选择性的让信息通过,其实际上就是一层全连接层,他的输入是一个向量,输出是一个0到1之间的使出向量,即$ g(x) = \sigma(Wx+b)$ 。在LSTM中主要有三个门结构,遗忘门、输入门和输出门。
门的使用,就是用门的输出向量按元素乘以我们需要控制的那个向量。因为门的输出是0到1之间的实数向量,所以门的值的大小就控制出信息的输出比例。
2.1 遗忘门

遗忘门决定了上一时刻的单元状态$ c_{t-1}$ 有多少可以保留到当前时刻$ c_t$ 中。
遗忘门在LSTM的位置以及计算公式如上图,其中$ W_f$ 是遗忘门的权重矩阵,$ [h_{t-1},x_t]$ 是两个输入的连接,$ b_f$ 是偏置。
如果$ x_t$ 的维度为$ d_x$ ,$ h_{t-1}$ 的维度为$ d_h$ , $ c_{t-1}$ 的维度为$ d_c$ (通常$ d_h = d_c$),那么,遗忘门的权重矩阵就是$ d_c \times (d_h + d_x)$ 。
2.2 输入门

输入门决定了当前时刻网络的输入$ x_t$ 有多少可以保存到单元状态$ c_t$ 中 。
其中,$ \tilde{C_t}$ 计算的是当前输入的特征信息,$ i_t$ 是输入门的输出,这两项点乘,就是该输入留下的信息。

把遗忘门和输入门加入到隐藏层中,结构如上图,运算得到的结果就是当前时刻的单元状态$ c_t$ 。
2.3 输出门

输出门决定了当前时刻的单元状态$ c_t$ 有多少输出到输出值$ h_t$ 中 。
通过输出门与$ c_t$ 的运算,其输出结果就是LSTM的输出
以上就是LSTM的前向传播过程,也就是LSTM的结构。
3、LSTM的优点
单元状态$ c_t$ 的引入不仅仅解决了RNN的梯度消失问题,同时,利用了门结构,协调了长期依赖与短期信息的关系。
4、LSTM变体之GRU
GRU是LSTM的简化,其结构图如下:

在GRU中,仅仅存在两个门,重置门和更新门。
其中,$ r_t$ 表示重置门,决定了到底有多少过去的信息需要遗忘。 $ z_t$ 表示更新门,决定了当前时刻的信息对输出的影响大小。
GRU虽然简化了很多,但是效果也是很不错的。